【题目】漳州市博物馆为了保护一件珍贵文物,需要在馆内一种透明又密封的长方体玻璃保护罩内充入保护液体.该博物馆需要支付的总费用由两部分组成:①罩内该种液体的体积比保护罩的容积少0.5立方米,且每立方米液体费用500元;②需支付一定的保险费用,且支付的保险费用与保护罩容积成反比,当容积为2立方米时,支付的保险费用为4000元.
(Ⅰ)求该博物馆支付总费用![]() 与保护罩容积
与保护罩容积![]() 之间的函数关系式;
之间的函数关系式;
(Ⅱ)求该博物馆支付总费用的最小值.
参考答案:
【答案】(Ⅰ)![]() (Ⅱ)博物馆支付总费用的最小值为3750元
(Ⅱ)博物馆支付总费用的最小值为3750元
【解析】【试题分析】(1)先依据题设分别求出支付的保险费用![]() 和保护液体的费用
和保护液体的费用![]() ,再求出运总费用
,再求出运总费用![]() 与保护罩容积
与保护罩容积![]() 之间的函数关系式
之间的函数关系式![]() ,(
,( ![]() );(2)依据题设条件运用基本不等式求出
);(2)依据题设条件运用基本不等式求出![]() 的最小值,从而确定函数
的最小值,从而确定函数![]() 的最小值:
的最小值:
解:(Ⅰ)由题意设支付的保险费用![]() ,把
,把![]() ,
, ![]() 代入,得
代入,得![]() .
.
则有支付的保险费用![]() (
(![]() )
)
故总费用![]() ,(
,( ![]() )
)
(Ⅱ)因为![]()
![]()
当且仅当![]() 且
且![]() ,
,
即![]() 立方米时不等式取等号,
立方米时不等式取等号,
所以,博物馆支付总费用的最小值为3750元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)求函数
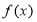 的单调区间;
的单调区间;(2)若
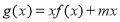 在区间
在区间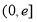 上的最大值为
上的最大值为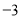 ,求
,求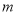 的值;
的值;(3)若
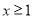 ,有不等式
,有不等式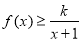 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
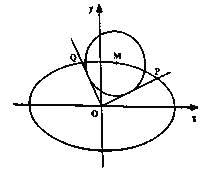
查看答案和解析>>【题目】如图,已知椭圆
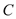 :
: 的离心率
的离心率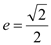 ,过点
,过点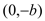 ,
,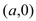 的直线与原点的距离为
的直线与原点的距离为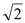 ,
,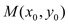 是椭圆上任一点,从原点
是椭圆上任一点,从原点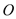 向圆
向圆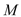 :
: 作两条切线,分别交椭圆于点
作两条切线,分别交椭圆于点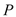 ,
,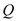 .
.
(Ⅰ)求椭圆
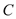 的方程;
的方程;(Ⅱ)若记直线
 ,
,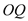 的斜率分别为
的斜率分别为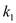 ,
,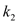 ,试求
,试求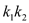 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法错误的是( )
A. 在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高
B. 在线性回归分析中,回归直线不一定过样本点的中心

C. 在回归分析中,
 为0.98的模型比
为0.98的模型比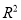 为0.80的模型拟合的效果好
为0.80的模型拟合的效果好D. 自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
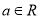 ,函数
,函数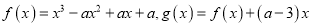 .
.(1)求证:曲线
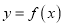 在点
在点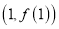 处的切线过定点;
处的切线过定点;(2)若
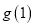 是
是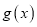 在区间
在区间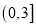 上的极大值,但不是最大值,求实数
上的极大值,但不是最大值,求实数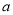 的取值范围;
的取值范围;(3)求证:对任意给定的正数
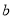 ,总存在
,总存在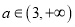 ,使得
,使得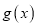 在
在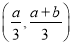 上为单调函数.
上为单调函数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
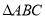 的三个顶点分别为是
的三个顶点分别为是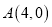 ,
,  ,
, 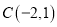 .
.(Ⅰ)求
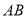 边上的高
边上的高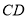 所在的直线方程;
所在的直线方程;(Ⅱ)求过点
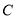 且在两坐标轴上的截距相等的直线方程.
且在两坐标轴上的截距相等的直线方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
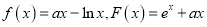 ,其中
,其中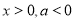 .
.(1)若
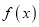 和
和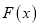 在区间
在区间 上具有相同的单调性,求实数
上具有相同的单调性,求实数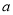 的取值范围;
的取值范围;(2)若
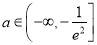 ,且函数
,且函数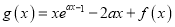 的最小值为
的最小值为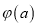 ,求
,求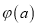 的最小值.
的最小值.
相关试题

