【题目】如图,在三棱锥V﹣ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=![]() ,O,M分别为AB,VA的中点.
,O,M分别为AB,VA的中点.
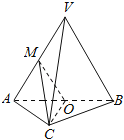
(1)求证:VB∥平面MOC;
(2)求证:平面MOC⊥平面VAB
(3)求三棱锥V﹣ABC的体积.
参考答案:
【答案】(1)证明解析;(2)证明见解析;(3)![]() .
.
【解析】试题分析:(1)由中位线定理可得OM∥BE,故而EB∥平面MOC;
(2)由等腰三角形三线合一可得OC⊥AB,由平面EAB⊥平面ABC可得OC⊥平面EAB,故而平面MOC⊥平面EAB;
(3)连结OE,则OE为棱锥的高,利用等边三角形的性质求出OE,代入体积计算.
证明:(1)证明:∵O,M分别为AB,EA的中点,∴OM∥BE,
又∵EB平面MOC,OM平面MOC,
∴EB∥平面MOC.
(2)∵AC=BC,O 为AB中点,∴OC⊥AB,
又∵平面EAB⊥平面ABC,平面EAB∩平面ABC=AB,
∴OC⊥平面EAB,又∵OC平面MOC,
∴平面MOC⊥平面 EAB.
(3)连结OE,则OE⊥AB,
又∵平面EAB⊥平面ABC,平面EAB∩平面ABC=AB,OE平面EAB,
∴OE⊥平面ABC.
∵AC⊥BC,AC=BC=![]() ,∴AB=2,
,∴AB=2,
∵三角形EAB为等边三角形,∴OE=![]() .
.
∴三棱锥E﹣ABC的体积V=![]() EO=
EO=![]() =
=![]() .
.
-
科目: 来源: 题型:
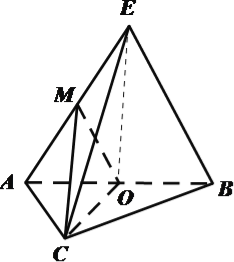
查看答案和解析>>【题目】如图,四面体
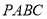 中,
中, 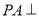 平面
平面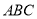 ,
, 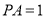 ,
, 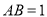 ,
,  ,
,  .
.(Ⅰ)求四面体
 的四个面的面积中,最大的面积是多少?
的四个面的面积中,最大的面积是多少?(Ⅱ)证明:在线段
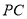 上存在点
上存在点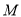 ,使得
,使得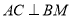 ,并求
,并求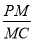 的值.
的值.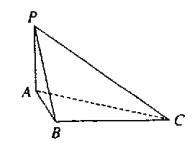
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
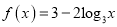 ,
, 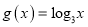 .
.(1)当
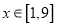 时,求函数
时,求函数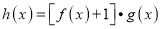 的值域;
的值域;(2)如果对任意的
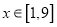 ,不等式
,不等式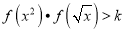 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;(3)是否存在实数
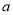 ,使得函数
,使得函数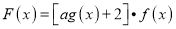 的最大值为0,若存在,求出
的最大值为0,若存在,求出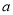 的值,若不存在,说明理由.
的值,若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知方程
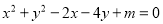 .
.(Ⅰ)若此方程表示圆,求
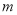 的取值范围;
的取值范围;(Ⅱ)若(Ⅰ)中的圆与直线
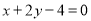 相交于
相交于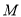 ,
, 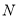 两点,且
两点,且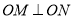 (
(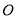 为坐标原点),求
为坐标原点),求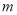 ;
;(Ⅲ)在(Ⅱ)的条件下,求以
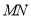 为直径的圆的方程.
为直径的圆的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知E,F分别是棱长为1的正方体ABCD﹣A1B1C1D1的棱BC,CC1的中点,则截面AEFD1与底面ABCD所成二面角的正弦值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业生产A,B两种产品,根据市场调查与预测,A产品的利润与投资成正比,其关系如图①;B产品的利润与投资的算术平方根成正比,其关系如图②.(注:利润和投资单位:万元)
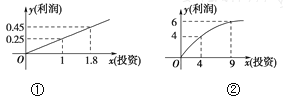
(1)分别将A,B两种产品的利润表示为投资的函数关系式;
(2)已知该企业已筹集到18万元资金,并将全部投入A,B两种产品的生产,怎样分配这18万元投资,才能使该企业获得最大利润?其最大利润约为多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段AB的端点A的坐标为
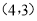 ,端点B是圆
,端点B是圆 :
: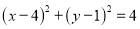 上的动点.
上的动点.(1)求过A点且与圆
 相交时的弦长为
相交时的弦长为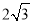 的直线
的直线 的方程。
的方程。(2)求线段AB中点M的轨迹方程,并说明它是什么图形。
相关试题

