【题目】已知函数![]() ,
,![]() (其中
(其中![]() ,
,![]() ,
,![]() )的图象的两条相邻对称轴之间的距离为
)的图象的两条相邻对称轴之间的距离为![]() ,且图象上一个最低点为
,且图象上一个最低点为![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)当![]() 时,求函数
时,求函数![]() 的值域;
的值域;
(3)若方程![]() 在
在![]() 上有两个不相等的实数根
上有两个不相等的实数根![]() ,求
,求![]() 的值.
的值.
参考答案:
【答案】(1)![]() ;(2)值域为
;(2)值域为![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据图象的最低点得到![]() ,由两相邻对称轴间的距离可得周期,进而得到
,由两相邻对称轴间的距离可得周期,进而得到![]() ,再根据代点法得到
,再根据代点法得到![]() ,于是可得解析式
,于是可得解析式![]() .(2)由
.(2)由![]() ,
,
得![]() ,然后结合正弦函数的图象可求得值域.(3)根据方程
,然后结合正弦函数的图象可求得值域.(3)根据方程![]() 在
在![]() 上有两个不相等的实数根
上有两个不相等的实数根![]() ,可得
,可得![]() ,于是
,于是![]() ,结合三角变换可得所求的函数值.
,结合三角变换可得所求的函数值.
(1)由函数图象的最低点为![]() 得
得![]() ,
,
由图象的两条相邻对称轴之间的距离为![]() 得
得![]() ,
,
∴![]() ,
,
∴![]() .
.
又点![]() 在函数的图象上,
在函数的图象上,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
又![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)∵![]() ,
,
∴![]() ,
,
当![]() ,即
,即![]() 时,
时,![]() 取得最大值1;
取得最大值1;
当![]() ,即
,即![]() 时,
时,![]() 取得最小值
取得最小值![]() .
.
故当![]() 时,函数
时,函数![]() 的值域为
的值域为![]()
(3)∵![]()
∴![]() ,
,
又方程![]() 在
在![]() 上有两个不相等的实数根
上有两个不相等的实数根![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列等式:
(sin )﹣2+(sin
)﹣2+(sin  )﹣2=
)﹣2=  ×1×2;
×1×2;
(sin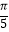 )﹣2+(sin
)﹣2+(sin  )﹣2+(sin
)﹣2+(sin  )﹣2+sin(
)﹣2+sin(  )﹣2=
)﹣2=  ×2×3;
×2×3;
(sin )﹣2+(sin
)﹣2+(sin  )﹣2+(sin
)﹣2+(sin  )﹣2+…+sin(
)﹣2+…+sin(  )﹣2=
)﹣2=  ×3×4;
×3×4;
(sin )﹣2+(sin
)﹣2+(sin  )﹣2+(sin
)﹣2+(sin  )﹣2+…+sin(
)﹣2+…+sin(  )﹣2=
)﹣2=  ×4×5;
×4×5;
…
照此规律,
(sin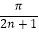 )﹣2+(sin
)﹣2+(sin  )﹣2+(sin
)﹣2+(sin  )﹣2+…+(sin
)﹣2+…+(sin  )﹣2= .
)﹣2= . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
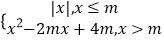 ,其中m>0,若存在实数b,使得关于x的方程f(x)=b有三个不同的根,则m的取值范围是 .
,其中m>0,若存在实数b,使得关于x的方程f(x)=b有三个不同的根,则m的取值范围是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】随着互联网的发展,移动支付(又称手机支付)越来越普遍,某学校兴趣小组为了了解移动支付在大众中的熟知度,对15-65岁的人群随机抽样调查,调查的问题是“你会使用移动支付吗?”其中,回答“会”的共有
 个人,把这
个人,把这 个人按照年龄分成5组:第1组
个人按照年龄分成5组:第1组 ,第2组
,第2组 ,第3组
,第3组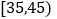 ,第4组
,第4组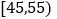 ,第5组
,第5组 ,然后绘制成如图所示的频率分布直方图,其中,第一组的频数为20.
,然后绘制成如图所示的频率分布直方图,其中,第一组的频数为20.
(1)求
 和
和 的值,并根据频率分布直方图估计这组数据的众数;
的值,并根据频率分布直方图估计这组数据的众数;(2)从第1,3,4组中用分层抽样的方法抽取6人,求第1,3,4组抽取的人数;
(3)在(2)抽取的6人中再随机抽取2人,求所抽取的2人来自同一个组的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某儿童节在“六一”儿童节推出了一项趣味活动.参加活动的儿童需转动如图所示的转盘两次,每次转动后,待转盘停止转动时,记录指针所指区域中的数.记两次记录的数分别为x,y.奖励规则如下:
①若xy≤3,则奖励玩具一个;
②若xy≥8,则奖励水杯一个;
③其余情况奖励饮料一瓶.
假设转盘质地均匀,四个区域划分均匀,小亮准备参加此项活动.
(1)求小亮获得玩具的概率;
(2)请比较小亮获得水杯与获得饮料的概率的大小,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 三个顶点坐标分别为:
三个顶点坐标分别为: 直线
直线 经过点
经过点
(1)求
 外接圆
外接圆 的方程.
的方程.(2)若直线
 与
与 相交于
相交于 两点,且
两点,且 ,求直线
,求直线 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
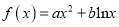 在
在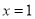 处有极值
处有极值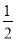 .
.(1)求
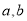 的值;
的值;(2)求
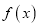 的单调区间.
的单调区间.
相关试题

