【题目】一个路口的红绿灯,红灯亮的时间为40秒,黄灯亮的时间为5秒,绿灯亮的时间为50秒(没有两灯同时亮),当你到达路口时,看见下列三种情况的概率各是多少?
(1)红灯;
(2)黄灯;
(3)不是红灯.
参考答案:
【答案】
(1)解:全部时间为40+5+50=95秒,每一时刻到达路口是等可能的,属于几何概型,
记“看见红灯”为事件A,“看见黄灯”为事件B,“看见绿灯”为事件C,“看见的不是红灯”为事件D,则P(A)= ![]()
(2)解:P(B)= ![]()
(3)解:P(D)=P(B)+P(C)= ![]()
【解析】根据几何概型的概率公式分别进行求解即可.
【考点精析】解答此题的关键在于理解几何概型的相关知识,掌握几何概型的特点:1)试验中所有可能出现的结果(基本事件)有无限多个;2)每个基本事件出现的可能性相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,如果执行如图所示的程序框图,输入n=6,m=4,那么输出的p= .
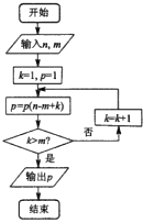
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=cosxsin(x+
 )﹣
)﹣ 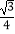 .
.
(Ⅰ)求f(x)的最小正周期;
(Ⅱ)△ABC中,角A,B,C所对的边为a,b,c,f( )=
)=  ,B=
,B=  ,a=1,求△ABC的面积.
,a=1,求△ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四棱锥P﹣ABCD中,PD⊥底面ABCD,且底面ABCD是边长为2的正方形,M、N分别为PB、PC的中点.

(1)证明:MN∥平面PAD;
(2)若PB与平面ABCD所成的角为45°,求三棱锥C﹣BDN的体积V. -
科目: 来源: 题型:
查看答案和解析>>【题目】20名学生某次数学考试成绩(单位:分)的频率分布直方图如图:
(Ⅰ)求频率分布直方图中a的值;
(Ⅱ)分别求出成绩落在[50,60)与[60,70)中的学生人数;
(Ⅲ)从成绩在[50,70)的学生任选2人,求此2人的成绩都在[60,70)中的概率.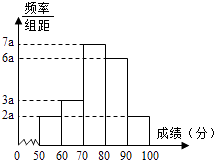
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
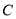 :
: 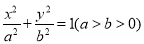 的长轴长为6,且椭圆
的长轴长为6,且椭圆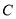 与圆
与圆 :
: 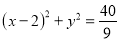 的公共弦长为
的公共弦长为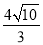 .
.(1)求椭圆
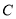 的方程.
的方程.(2)过点
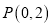 作斜率为
作斜率为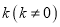 的直线
的直线 与椭圆
与椭圆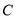 交于两点
交于两点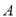 ,
,  ,试判断在
,试判断在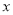 轴上是否存在点
轴上是否存在点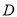 ,使得
,使得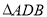 为以
为以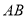 为底边的等腰三角形.若存在,求出点
为底边的等腰三角形.若存在,求出点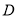 的横坐标的取值范围,若不存在,请说明理由.
的横坐标的取值范围,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:x2+4y2=16,点M(2,1).
(1)求椭圆C的焦点坐标和离心率;
(2)求通过M点且被这点平分的弦所在的直线方程.
相关试题

