【题目】过点![]() 作一直线与抛物线
作一直线与抛物线![]() 交于
交于![]() 两点,点
两点,点![]() 是抛物线
是抛物线![]() 上到直线
上到直线![]() :
: ![]() 的距离最小的点,直线
的距离最小的点,直线![]() 与直线
与直线![]() 交于点
交于点![]() .
.
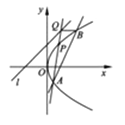
(Ⅰ)求点![]() 的坐标;
的坐标;
(Ⅱ)求证:直线![]() 平行于抛物线的对称轴.
平行于抛物线的对称轴.
参考答案:
【答案】(Ⅰ) ![]() ;(Ⅱ)证明见解析.
;(Ⅱ)证明见解析.
【解析】试题分析:(Ⅰ)到直线![]() 距离最小的点,可根据点到直线距离公式,取最小值时的点;也可根据几何意义得为与直线
距离最小的点,可根据点到直线距离公式,取最小值时的点;也可根据几何意义得为与直线![]() 平行且与抛物线相切的切点:如根据点
平行且与抛物线相切的切点:如根据点![]() 到直线
到直线![]() 的距离
的距离
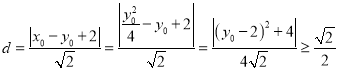 得当且仅当
得当且仅当![]() 时取最小值,(Ⅱ)要证直线
时取最小值,(Ⅱ)要证直线![]() 平行于抛物线的对称轴,就是要证
平行于抛物线的对称轴,就是要证![]() 两点纵坐标相等,设点
两点纵坐标相等,设点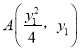 ,求出直线AP方程
,求出直线AP方程![]() ,与直线
,与直线![]() 方程联立,解出点
方程联立,解出点![]() 纵坐标为
纵坐标为![]() .同理求出直线AB方程
.同理求出直线AB方程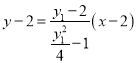 ,与抛物线方程联立,解出点
,与抛物线方程联立,解出点![]() 纵坐标为
纵坐标为![]() .
.
试题解析:(Ⅰ)设点![]() 的坐标为
的坐标为![]() ,则
,则![]() ,
,
所以,点![]() 到直线
到直线![]() 的距离
的距离
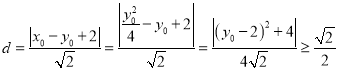 .
.
当且仅当![]() 时等号成立,此时
时等号成立,此时![]() 点坐标为
点坐标为![]() .………………………………4分
.………………………………4分
(Ⅱ)设点![]() 的坐标为
的坐标为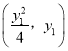 ,显然
,显然![]() .
.
当![]() 时,
时, ![]() 点坐标为
点坐标为![]() ,直线
,直线![]() 的方程为
的方程为![]() ;
;
当![]() 时,直线
时,直线![]() 的方程为
的方程为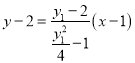 ,
,
化简得![]() ;
;
综上,直线![]() 的方程为
的方程为![]() .
.
与直线![]() 的方程
的方程![]() 联立,可得点
联立,可得点![]() 的纵坐标为
的纵坐标为![]() .
.
当![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,可得
,可得![]() 点的纵坐标为
点的纵坐标为![]() .
.
此时![]() ,
,
即知![]() 轴,
轴,
当![]() 时,直线
时,直线![]() 的方程为
的方程为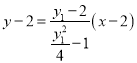 ,
,
化简得![]() ,
,
与抛物线方程![]() 联立,消去
联立,消去![]() ,
,
可得![]() ,
,
所以点![]() 的纵坐标为
的纵坐标为![]() .
.
从而可得![]() 轴,
轴,
所以, ![]() 轴.……………………………………13分
轴.……………………………………13分
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
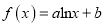 (
(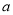 ,
, 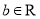 ),曲线
),曲线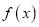 在
在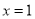 处的切线方程为
处的切线方程为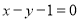 .
.(Ⅰ)求
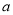 ,
, 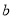 的值;
的值;(Ⅱ)证明:
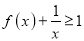 ;
;(Ⅲ)已知满足
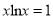 的常数为
的常数为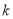 .令函数
.令函数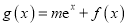 (其中
(其中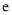 是自然对数的底数,
是自然对数的底数, 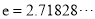 ),若
),若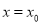 是
是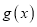 的极值点,且
的极值点,且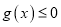 恒成立,求实数
恒成立,求实数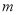 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥P﹣ABCD的底面ABCD是矩形,平面PAB⊥平面ABCD,PA=AB=3,BC=2,E、F分别是棱AD,PC的中点
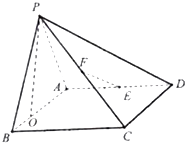
(1)求证:EF⊥平面PBC
(2)若直线PC与平面ABCD所成角为 ,点P在AB上的射影O在靠近点B的一侧,求二面角P﹣EF﹣A的余弦值.
,点P在AB上的射影O在靠近点B的一侧,求二面角P﹣EF﹣A的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=xln(x+
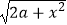 (a>0)为偶函数.
(a>0)为偶函数.
(1)求a的值;
(2)求g(x)=ax2+2x+1在区间[﹣6,3]上的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知圆G:x2﹣x+y2=0,经过抛物线y2=2px的焦点,过点(m,0)(m<0)倾斜角为
 的直线l交抛物线于C,D两点. (Ⅰ)求抛物线的方程;
的直线l交抛物线于C,D两点. (Ⅰ)求抛物线的方程;
(Ⅱ)若焦点F在以线段CD为直径的圆E的外部,求m的取值范围.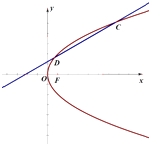
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
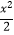 +y2=1的左右焦点分别为F1 , F2 , 直线l过椭圆的右焦点F2与椭圆交于A,B 两点, (Ⅰ)当直线l的斜率为1,点P为椭圆上的动点,满足使得△ABP的面积为
+y2=1的左右焦点分别为F1 , F2 , 直线l过椭圆的右焦点F2与椭圆交于A,B 两点, (Ⅰ)当直线l的斜率为1,点P为椭圆上的动点,满足使得△ABP的面积为 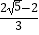 的点P有几个?并说明理由.
的点P有几个?并说明理由.
(Ⅱ)△ABF1的内切圆的面积是否存在最大值?若存在,求出这个最大值及此时直线l的方程,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某小区提倡低碳生活,环保出行,在小区提供自行车出租.该小区有40辆自行车供小区住户租赁使用,管理这些自行车的费用是每日92元,根据经验,若每辆自行车的日租金不超过5元,则自行车可以全部出租,若超过5元,则每超过1元,租不出的自行车就增加2辆,为了便于结算,每辆自行车的日租金x元只取整数,用f(x)元表示出租自行车的日纯收入(日纯收入=一日出租自行车的总收入﹣管理费用)
(1)求函数f(x)的解析式及其定义域;
(2)当租金定为多少时,才能使一天的纯收入最大?
相关试题

