【题目】设双曲线C的焦点在![]() 轴上,离心率为
轴上,离心率为![]() ,其一个顶点的坐标是(0,1).
,其一个顶点的坐标是(0,1).
(Ⅰ)求双曲线C的标准方程;
(Ⅱ)若直线![]() 与该双曲线交于A、B两点,且A、B的中点为(2,3),求直线
与该双曲线交于A、B两点,且A、B的中点为(2,3),求直线![]() 的方程
的方程
参考答案:
【答案】(1) ![]() (2)
(2) ![]()
【解析】试题分析:(Ⅰ)由顶点坐标是(0,3),求得a,由已知条件双曲线的离心率为![]() ,列出方程求出c,利用双曲线的三参数的关系,求出b,据双曲线焦点的位置写出双曲线的方程.
,列出方程求出c,利用双曲线的三参数的关系,求出b,据双曲线焦点的位置写出双曲线的方程.
(Ⅱ)设出A,B的坐标,代入双曲线方程,两式相减,根据中点的坐标可知x1+x2和y1+y2的值,进而求得直线AB的斜率,根据点斜式求得直线的方程.
试题解析:
(1)由已知得 ![]()
又![]() ∴
∴![]()
∴ 双曲线C的标准方程为![]()
(2) 设A、B两点的坐标分别为![]() 、
、![]() ,
,
则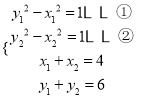 由①-②得:
由①-②得: ![]()
∴![]() .
.
∴直线![]() 的方程为
的方程为![]() 经检验满足。
经检验满足。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
 中,圆
中,圆 :
: 与
与 轴的正半轴交于点
轴的正半轴交于点 ,以点
,以点 为圆心的圆
为圆心的圆 :
: 与圆
与圆 交于
交于 ,
, 两点.
两点.(1)当
 时,求
时,求 的长;
的长;(2)当
 变化时,求
变化时,求 的最小值;
的最小值;(3)过点
 的直线
的直线 与圆A切于点
与圆A切于点 ,与圆
,与圆 分别交于点
分别交于点 ,
, ,若点
,若点 是
是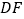 的中点,试求直线
的中点,试求直线 的方程.
的方程. 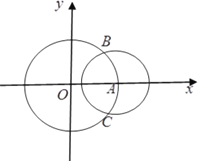
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校有
 名学生参加学校组织的“数学竞赛集训队”选拔考试,现从中等可能抽出
名学生参加学校组织的“数学竞赛集训队”选拔考试,现从中等可能抽出 名学生的成绩作为样本,制成如图频率分布表:
名学生的成绩作为样本,制成如图频率分布表:分组
频数
频率

0.025

0.050

0.200
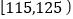
12
0.300

0.275

4

0.00
合计

1
(1)求
 的值,并根据题中信息估计总体平均数是多少?
的值,并根据题中信息估计总体平均数是多少?(2)若成绩不低于
 分的同学能参加“数学竞赛集训队”,试估计该校大约多少名学生能参加“数学竞赛集训队”?
分的同学能参加“数学竞赛集训队”,试估计该校大约多少名学生能参加“数学竞赛集训队”? -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系,圆C的极坐标方程为ρ=2
 cos
cos ,直线l的参数方程为
,直线l的参数方程为 (t为参数),直线l与圆C交于A,B两点,P是圆C上不同于A,B的任意一点.
(t为参数),直线l与圆C交于A,B两点,P是圆C上不同于A,B的任意一点.(1)求圆心的极坐标;
(2)求△PAB面积的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知动圆
 过点
过点 ,且与圆
,且与圆 相内切.
相内切.(I)求动圆
 的圆心的轨迹方程;
的圆心的轨迹方程;(II)设直线
 (其中
(其中 与(1)中所求轨迹交于不同两点
与(1)中所求轨迹交于不同两点 ,D,与双曲线
,D,与双曲线 交于不同两点
交于不同两点 ,问是否存在直线
,问是否存在直线 ,使得向量
,使得向量 ,若存在,指出这样的直线有多少条?若不存在,请说明理由.
,若存在,指出这样的直线有多少条?若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (
( 为实常数) .
为实常数) .(I)当
 时,求函数
时,求函数 在
在 上的最大值及相应的
上的最大值及相应的 值;
值;(II)当
 时,讨论方程
时,讨论方程 根的个数.
根的个数.(III)若
 ,且对任意的
,且对任意的 ,都有
,都有 ,求
,求实数a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列
 满足
满足 ,
,  .
.(1)求
 的通项公式;
的通项公式; (2)各项均为正数的等比数列
 中,
中,  ,
,  ,求
,求 的前
的前 项和
项和 .
.
相关试题

