【题目】已知函数![]() .
.
(1)若任意![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(2)求证:对任意![]() ,
, ![]() ,都有
,都有![]() 成立;
成立;
(3)对于给定的正数![]() ,有一个最大的正数
,有一个最大的正数![]() ,使得整个区间
,使得整个区间![]() 上,不等式
上,不等式![]() 恒成立,求出
恒成立,求出![]() 的解析式.
的解析式.
参考答案:
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)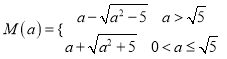
【解析】试题分析:
(1)由题意令![]() ,则
,则![]() ,可得
,可得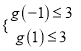 ,即可求解实数
,即可求解实数![]() 的取值范围;
的取值范围;
(2)对任意![]() ,
, ![]() ,作差化简
,作差化简![]() ,即可.
,即可.
(3)由题意得![]() ,由不等式
,由不等式![]() 恒成立得
恒成立得![]() 且
且![]() ,结合二次函数的图象,分类讨论,即可求解
,结合二次函数的图象,分类讨论,即可求解![]() 的表达式.
的表达式.
试题解析:
(1)因为![]() ,
, ![]() 恒成立,令
恒成立,令![]() ,
, ![]() ,则
,则![]()
所以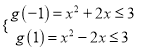 ,解得
,解得![]()
(2)对任意![]() ,
, ![]() ,
,
![]()
![]()
![]()
![]()
![]() ,
, ![]()
(3)![]() 对称轴
对称轴![]() ,
, ![]() 由不等式
由不等式![]() 恒成立得
恒成立得![]() 且
且![]()
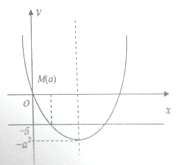
因为![]() ,当
,当![]() ,即
,即![]() 时,则
时,则![]() ,
, ![]() 在
在![]() 为减函数.
为减函数.
由题意知: ![]() 由
由![]() 且
且![]() ,解得:
,解得: ![]()
所以![]() 时,
时, ![]()
当![]() ,即
,即![]() 时,则
时,则![]() 总成立
总成立![]()
由题意得: ![]() ,
, ![]() 在
在![]() 为减函数,
为减函数, ![]() 在
在![]() 为增函数,
为增函数,
又![]() ,则
,则![]() ,
, ![]()
由![]() ,
, ![]() 解得
解得![]() ,所以
,所以![]() 时,
时, ![]()
综上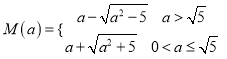
点睛:本题考查了函数的综合应用,解答中涉及到不等式的恒成立问题的求解,不等式的性质的应用,以及二次函数的图象与性质的应用,解答中把不等式的恒成立问题转化为函数的最值问题是解答的关键,试题综合性强,属于中档试题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】长方体ABCD﹣A1B1C1D1中,AB=2,AA1=AD=4,点E为AB中点.
(1)求证:BD1∥平面A1DE;
(2)求证:A1D⊥平面ABD1 .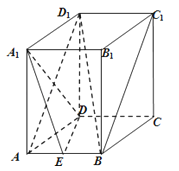
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
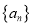 的前
的前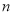 项和为
项和为 ,满足
,满足 与
与 的等差中项为
的等差中项为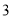 (
( ).
).(1)求数列
 的通项公式;
的通项公式;(2)是否存在正整数
 ,是不等式
,是不等式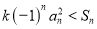 (
(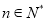 )恒成立,若存在,求出
)恒成立,若存在,求出 的最大值;若不存在,请说明理由.
的最大值;若不存在,请说明理由.(3)设

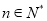 ,若集合
,若集合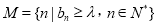 恰有
恰有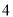 个元素,求实数
个元素,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】数列
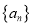 ,定义
,定义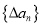 为数列
为数列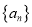 的一阶差分数列,其中
的一阶差分数列,其中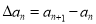 ,(
,( 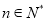 ),设
),设
(1)若
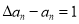 ,求证:
,求证: 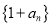 是等比数列,并求出
是等比数列,并求出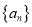 的通项公式;
的通项公式;(2)若
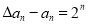 ,又数列
,又数列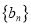 满足:
满足: 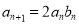 :
:①求数列
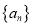 的前
的前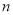 和
和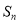 ;
;②求证:数列
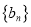 中的任意一项总可以表示成该数列中其他两项之积.
中的任意一项总可以表示成该数列中其他两项之积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)若
 ,求函数
,求函数 的极值;
的极值;(2)若函数
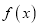 有两个零点,求实数
有两个零点,求实数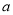 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设
 .
.(1)求
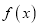 的单调区间;
的单调区间;(2)已知
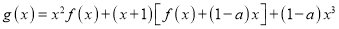 ,若对所有
,若对所有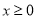 ,都有
,都有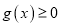 成立,求实数
成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
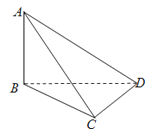
查看答案和解析>>【题目】在三棱锥A﹣BCD中,AB⊥平面BCD,BC⊥CD,且AB=3,BD=4,则三棱锥A﹣BCD外接球的半径为( )
A.2
B.3
C.4
D.
相关试题

