【题目】已知函数![]() .
.
(1)若![]() ,求函数
,求函数![]() 的极值;
的极值;
(2)若函数![]() 有两个零点,求实数
有两个零点,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() 时,
时, ![]() 取极大值
取极大值![]() ;当
;当![]() 时,
时, ![]() 取极小值
取极小值![]() ;(2)实数
;(2)实数![]() 的取值范围是
的取值范围是![]() 。
。
【解析】试题分析:(1)函数求导得![]() ,讨论导数的单调性即可得极值;
,讨论导数的单调性即可得极值;
(2)函数求导得![]() ,讨论
,讨论![]() ,
, ![]() ,
, ![]() 和
和![]() 时函数的单调性及最值即可下结论.
时函数的单调性及最值即可下结论.
试题解析:
(1)函数定义域为![]() ,
, ![]() .
.
![]() ,解得
,解得![]() ,
, ![]() ,
,
列表:
|
|
|
|
|
|
|
|
|
|
|
|
|
| 极大值 |
| 极小值 |
|
所以![]() 时,
时, ![]() 取极大值
取极大值![]() ;当
;当![]() 时,
时, ![]() 取极小值
取极小值![]() .
.
(2)![]() ,
,
当![]() 时,易知函数
时,易知函数![]() 只有一个零点,不符合题意;
只有一个零点,不符合题意;
当![]() 时,在
时,在![]() 上,
上, ![]() ,
, ![]() 单调递减;
单调递减;
在![]() 上,
上, ![]() ,
, ![]() 单调递增;
单调递增;
![]() ,且
,且![]() ,
, ![]() →
→![]() ,
, ![]() →
→![]() ,
,
所以函数![]() 有两个零点.
有两个零点.
当![]() 时,在
时,在![]() 和
和![]() 上,
上, ![]() ,
, ![]() 单调递增;在
单调递增;在![]() 上
上![]() ,
, ![]() 单调递减;
单调递减;
![]() ,函数
,函数![]() 至多有一个零点,不符合题意.
至多有一个零点,不符合题意.
当![]() 时,在
时,在![]() 和
和![]() 上
上![]() ,
, ![]() 单调递增;在
单调递增;在![]() 上
上![]() ,
, ![]() 单调递减;
单调递减;
![]() ,函数
,函数![]() 至多有一个零点,不符合题意.
至多有一个零点,不符合题意.
综上:实数![]() 的取值范围是
的取值范围是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
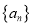 的前
的前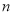 项和为
项和为 ,满足
,满足 与
与 的等差中项为
的等差中项为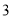 (
( ).
).(1)求数列
 的通项公式;
的通项公式;(2)是否存在正整数
 ,是不等式
,是不等式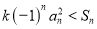 (
(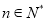 )恒成立,若存在,求出
)恒成立,若存在,求出 的最大值;若不存在,请说明理由.
的最大值;若不存在,请说明理由.(3)设

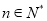 ,若集合
,若集合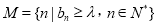 恰有
恰有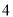 个元素,求实数
个元素,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】数列
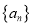 ,定义
,定义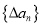 为数列
为数列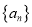 的一阶差分数列,其中
的一阶差分数列,其中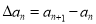 ,(
,( 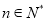 ),设
),设
(1)若
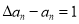 ,求证:
,求证: 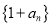 是等比数列,并求出
是等比数列,并求出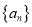 的通项公式;
的通项公式;(2)若
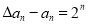 ,又数列
,又数列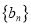 满足:
满足: 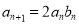 :
:①求数列
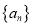 的前
的前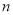 和
和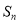 ;
;②求证:数列
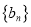 中的任意一项总可以表示成该数列中其他两项之积.
中的任意一项总可以表示成该数列中其他两项之积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
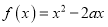 .
.(1)若任意
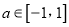 ,不等式
,不等式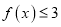 恒成立,求实数
恒成立,求实数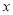 的取值范围;
的取值范围;(2)求证:对任意
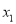 ,
, 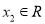 ,都有
,都有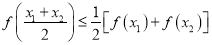 成立;
成立;(3)对于给定的正数
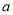 ,有一个最大的正数
,有一个最大的正数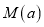 ,使得整个区间
,使得整个区间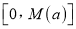 上,不等式
上,不等式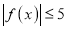 恒成立,求出
恒成立,求出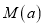 的解析式.
的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】设
 .
.(1)求
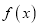 的单调区间;
的单调区间;(2)已知
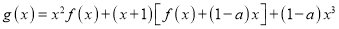 ,若对所有
,若对所有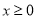 ,都有
,都有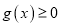 成立,求实数
成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在三棱锥A﹣BCD中,AB⊥平面BCD,BC⊥CD,且AB=3,BD=4,则三棱锥A﹣BCD外接球的半径为( )
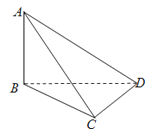
A.2
B.3
C.4
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2015 年 12 月,华中地区数城市空气污染指数“爆表”,此轮污染为 2015 年以来最严重的污染过程,为了探究车流量与
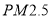 的浓度是否相关,现采集到华中某城市 2015 年 12 月份某星期星期一到星期日某一时间段车流量与
的浓度是否相关,现采集到华中某城市 2015 年 12 月份某星期星期一到星期日某一时间段车流量与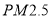 的数据如表:
的数据如表:时间
星期一
星期二
星期三
星期四
星期五
星期六
星期日
车流量
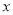 (万辆)
(万辆)1
2
3
4
5
6
7
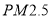 的浓度
的浓度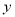 (微克/立方米)
(微克/立方米)28
30
35
41
49
56
62
(1)由散点图知
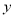 与
与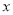 具有线性相关关系,求
具有线性相关关系,求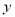 关于
关于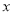 的线性回归方程;(提示数据:
的线性回归方程;(提示数据: 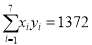 )
)(2)利用(1)所求的回归方程,预测该市车流量为 12 万辆时
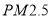 的浓度.
的浓度.参考公式:回归直线的方程是
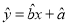 ,
,其中
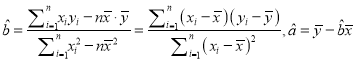 .
.
相关试题

