【题目】长方体ABCD﹣A1B1C1D1中,AB=2,AA1=AD=4,点E为AB中点.
(1)求证:BD1∥平面A1DE;
(2)求证:A1D⊥平面ABD1 . 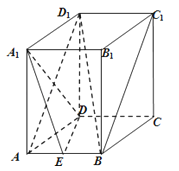
参考答案:
【答案】证明:(1)连结A1D,AD1 , A1D∩AD1=O,连结OE,
∵长方体ABCD﹣A1B1C1D1中,ADD1A1是矩形,
∴O是AD1的中点,∴OE∥BD1 ,
∵OE∥BD1 , OE平面ABD1 , BD1平面ABD1 ,
∴BD1∥平面A1DE.
(2)∵长方体ABCD﹣A1B1C1D1中,AB=2,AA1=AD=4,点E为AB中点,
∴ADD1A1是正方形,∴A1D⊥AD1 ,
∵长方体ABCD﹣A1B1C1D1中,AB⊥平面ADD1A1 ,
∴A1D⊥AB,
又AB∩AD1=A,∴A1D⊥平面ABD1 . 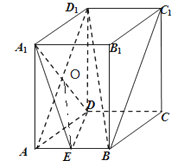
【解析】(1)连结A1D,AD1 , A1D∩AD1=O,连结OE,推导出OE∥BD1 , 由此能证明BD1∥平面A1DE.
(2)推导出A1D⊥AD1 , A1D⊥AB,由此能证明A1D⊥平面ABD1 .
-
科目: 来源: 题型:
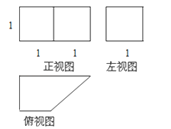
查看答案和解析>>【题目】已知一个几何体的三视图如下图,大致画出它的直观图,并求出它的表面积和体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
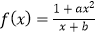 的图象经过点(1,3),并且g(x)=xf(x)是偶函数.
的图象经过点(1,3),并且g(x)=xf(x)是偶函数.
(1)求实数a、b的值;
(2)用定义证明:函数g(x)在区间(1,+∞)上是增函数. -
科目: 来源: 题型:
查看答案和解析>>【题目】某单位用2160万元购得一块空地,计划在该地块上建造一栋至少10层,每层2000平方米的楼房.经测算,如果将楼房建为x(x≥10)层,则每平方米的平均建筑费用为560+48x(单位:元).
(1)写出楼房平均综合费用y关于建造层数x的函数关系式;
(2)该楼房应建造多少层时,可使楼房每平方米的平均综合费用最少?最少值是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
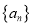 的前
的前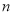 项和为
项和为 ,满足
,满足 与
与 的等差中项为
的等差中项为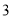 (
( ).
).(1)求数列
 的通项公式;
的通项公式;(2)是否存在正整数
 ,是不等式
,是不等式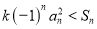 (
(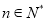 )恒成立,若存在,求出
)恒成立,若存在,求出 的最大值;若不存在,请说明理由.
的最大值;若不存在,请说明理由.(3)设

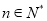 ,若集合
,若集合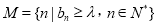 恰有
恰有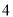 个元素,求实数
个元素,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】数列
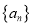 ,定义
,定义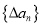 为数列
为数列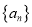 的一阶差分数列,其中
的一阶差分数列,其中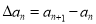 ,(
,( 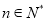 ),设
),设
(1)若
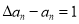 ,求证:
,求证: 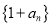 是等比数列,并求出
是等比数列,并求出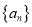 的通项公式;
的通项公式;(2)若
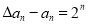 ,又数列
,又数列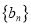 满足:
满足: 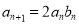 :
:①求数列
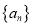 的前
的前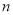 和
和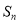 ;
;②求证:数列
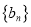 中的任意一项总可以表示成该数列中其他两项之积.
中的任意一项总可以表示成该数列中其他两项之积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
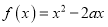 .
.(1)若任意
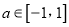 ,不等式
,不等式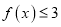 恒成立,求实数
恒成立,求实数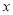 的取值范围;
的取值范围;(2)求证:对任意
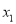 ,
, 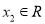 ,都有
,都有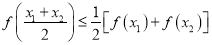 成立;
成立;(3)对于给定的正数
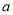 ,有一个最大的正数
,有一个最大的正数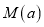 ,使得整个区间
,使得整个区间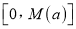 上,不等式
上,不等式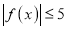 恒成立,求出
恒成立,求出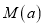 的解析式.
的解析式.
相关试题

