【题目】已知函数![]() .
.
(1)设函数![]() ,求函数
,求函数![]() 的单调区间;
的单调区间;
(2)若在区间![]() 上不存在
上不存在![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)当![]() 时,函数
时,函数![]() 的单调递增区间是
的单调递增区间是![]() ,当
,当![]() 时,函数
时,函数![]() 的单调递减区间是
的单调递减区间是![]() ,单调递增区间是
,单调递增区间是![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)通过分类讨论,确定单调区间;(2)正难则反,转化为恒成立问题,然后再通过分类讨论,求![]() 的取值范围.
的取值范围.
试题解析:(1)![]() ,∴
,∴![]()
①当![]() 时,
时,![]() ,∴
,∴![]() 在
在![]() 上递增;
上递增;
②当![]() 时,
时,![]() ,
,
∴![]() 在
在![]() 上递减,在
上递减,在![]() 上递增;
上递增;
(2)不存在![]() ,使得
,使得![]() 成立,
成立,
![]() 在
在![]() 上恒成立
上恒成立![]() 当
当![]() 时,
时,![]() ,
,
由(1)知:
①当![]() 时,
时,![]() 在
在![]() 上递增,∴
上递增,∴![]() ,∴
,∴![]() ,
,
②当![]() 时,
时,![]() 在
在![]() 上递减,在
上递减,在![]() 上递增;
上递增;
(i)当![]() 时,
时,![]() 在
在![]() 上递增,∴
上递增,∴![]() ,∴
,∴![]()
(ii)当![]() 时,
时,![]() 在
在![]() 上递减;
上递减;
∴![]() ,∴
,∴![]() ;
;
(iii)当![]() 时,
时,![]() 在
在![]() 上递减,在
上递减,在![]() 上递增;
上递增;
∴![]() ,
,
∴![]()
综上![]() ,
,
所以不存在一点![]() ,使得
,使得![]() 成立,实数
成立,实数![]() 的取值范围为
的取值范围为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下说法正确的是( )
A.零向量没有方向
B.单位向量都相等
C.共线向量又叫平行向量
D.任何向量的模都是正实数
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知过原点
 的动直线
的动直线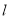 与圆
与圆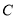 :
: 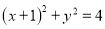 交于
交于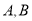 两点.
两点.(1)若
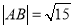 ,求直线
,求直线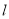 的方程;
的方程;(2)
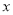 轴上是否存在定点
轴上是否存在定点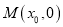 ,使得当
,使得当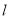 变动时,总有直线
变动时,总有直线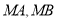 的斜率之和为0?若存在,求出
的斜率之和为0?若存在,求出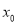 的值;若不存在,说明理由.
的值;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在三棱柱
 中,侧棱与底面垂直,
中,侧棱与底面垂直,  ,点
,点 分别为
分别为 和
和 的中点.
的中点.
(1)证明:
 平面
平面 ;
;证明:
 平面
平面 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
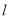 过点
过点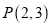 ,根据下列条件分别求出直线
,根据下列条件分别求出直线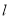 的方程:
的方程:(1)直线
 的倾斜角为
的倾斜角为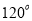 ;
;(2)
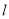 与直线x-2y+1=0垂直;
与直线x-2y+1=0垂直; (3)
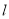 在
在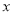 轴、
轴、 轴上的截距之和等于0.
轴上的截距之和等于0. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三棱柱
 的侧面
的侧面 是边长为1的正方形,侧面
是边长为1的正方形,侧面 侧面
侧面 是
是 的中点.
的中点.
(1)求证:
 平面
平面 ;
;(2)求证:
 平面
平面 ;
;(3)在线段
 上是否存在一点
上是否存在一点 ,使二面角
,使二面角 为45°,若存在,求
为45°,若存在,求 的长;若不存在,说明理由.
的长;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)当
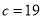 时,解关于
时,解关于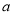 的不等式
的不等式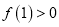 ;
;(2)若关于
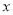 的不等式
的不等式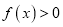 的解集是
的解集是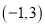 ,求实数
,求实数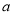 、
、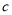 的值.
的值.
相关试题

