【题目】已知过原点![]() 的动直线
的动直线![]() 与圆
与圆![]() :
: ![]() 交于
交于![]() 两点.
两点.
(1)若![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得当
,使得当![]() 变动时,总有直线
变动时,总有直线![]() 的斜率之和为0?若存在,求出
的斜率之和为0?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)先求出圆心C(-1,0)到直线l的距离为![]() ,利用点到直线距离公式能求出直线l的方程.
,利用点到直线距离公式能求出直线l的方程.
(2)设![]() ,直线MA、MB的斜率分别为k1,k2.设l的方程为y=kx,代入圆C的方程得(k2+1)x2+2x-3=0,由此利用韦达定理,结果已知条件能求出存在定点M(3,0),使得当l变动时,总有直线MA、MB的斜率之和为0.
,直线MA、MB的斜率分别为k1,k2.设l的方程为y=kx,代入圆C的方程得(k2+1)x2+2x-3=0,由此利用韦达定理,结果已知条件能求出存在定点M(3,0),使得当l变动时,总有直线MA、MB的斜率之和为0.
试题解析:
(Ⅰ)设圆心![]() 到直线
到直线![]() 的距离为
的距离为![]() ,则
,则
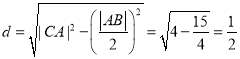
当![]() 的斜率不存在时,
的斜率不存在时, ![]() ,不合题意
,不合题意
当![]() 的斜率存在时,设
的斜率存在时,设![]() 的方程为
的方程为![]() ,由点到直线距离公式得
,由点到直线距离公式得
![]()
解得![]() ,故直线
,故直线![]() 的方程为
的方程为![]()
(Ⅱ)存在定点![]() ,且
,且![]() ,证明如下:
,证明如下:
设![]() ,直线
,直线![]() 、
、![]() 的斜率分别为
的斜率分别为![]() .
.
当![]() 的斜率不存在时,由对称性可得
的斜率不存在时,由对称性可得![]() ,
, ![]() ,符合题意
,符合题意
当![]() 的斜率存在时,设
的斜率存在时,设![]() 的方程为
的方程为![]() ,代入圆
,代入圆![]() 的方程
的方程
整理得![]()
∴![]() ,
, ![]() ,
,
∴![]()
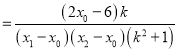
当![]() ,即
,即![]() 时,有
时,有![]() ,
,
所以存在定点![]() 符合题意,
符合题意, ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为贯彻落实教育部等
 部门《关于加快发展青少年校园足球的实施意见》,全面提高我市中学生的体质健康水平,普及足球知识和技能,市教体局决定举行春季校园足球联赛,为迎接此次联赛,甲中学选拔了
部门《关于加快发展青少年校园足球的实施意见》,全面提高我市中学生的体质健康水平,普及足球知识和技能,市教体局决定举行春季校园足球联赛,为迎接此次联赛,甲中学选拔了 名学生组成集训队,现统计了这
名学生组成集训队,现统计了这 名学生的身高,记录如下表:
名学生的身高,记录如下表:身高








人数








(1)请计算这
 名学生的身高中位数、众数,并补充完成下面的茎叶图:
名学生的身高中位数、众数,并补充完成下面的茎叶图:
(2)身高为
 和
和 的四名学生分别为
的四名学生分别为 ,现从这四名学生中选
,现从这四名学生中选 名担任正副门将,请利用列举法列出所有可能情况,并求学生
名担任正副门将,请利用列举法列出所有可能情况,并求学生 入选正门将的概率.
入选正门将的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】总体由编号为01,02,…,19,20的20个个体组成.利用下面的随机数表选取4个个体,选取方法从随机数表的第1行第4列数由左到右由上到下开始读取,则选出来的第4个个体的编号为( )
第1行 78 16 65 71 02 30 60 14 01 02 40 60 90 28 01 98
第2行 32 04 92 34 49 35 82 00 36 23 48 69 69 38 74 81
A.10B.01C.09D.06
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下说法正确的是( )
A.零向量没有方向
B.单位向量都相等
C.共线向量又叫平行向量
D.任何向量的模都是正实数
-
科目: 来源: 题型:
查看答案和解析>>【题目】在三棱柱
 中,侧棱与底面垂直,
中,侧棱与底面垂直,  ,点
,点 分别为
分别为 和
和 的中点.
的中点.
(1)证明:
 平面
平面 ;
;证明:
 平面
平面 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
. (1)设函数
 ,求函数
,求函数 的单调区间;
的单调区间;(2)若在区间
 上不存在
上不存在 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
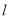 过点
过点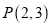 ,根据下列条件分别求出直线
,根据下列条件分别求出直线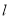 的方程:
的方程:(1)直线
 的倾斜角为
的倾斜角为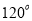 ;
;(2)
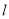 与直线x-2y+1=0垂直;
与直线x-2y+1=0垂直; (3)
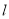 在
在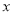 轴、
轴、 轴上的截距之和等于0.
轴上的截距之和等于0.
相关试题

