【题目】已知椭圆![]() 的中心在坐标原点
的中心在坐标原点![]() ,焦点在
,焦点在![]() 轴上,椭圆
轴上,椭圆![]() 的短轴端点和焦点所组成的四边形为正方形,且椭圆
的短轴端点和焦点所组成的四边形为正方形,且椭圆![]() 上任意一点到两个焦点的距离之和为
上任意一点到两个焦点的距离之和为![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)若直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,求
两点,求![]() 面积的最大值.
面积的最大值.
参考答案:
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ) ![]() .
.
【解析】试题分析:(1)由椭圆定义得![]() ,又椭圆
,又椭圆![]() 的短轴端点和焦点所组成的四边形为正方形,由椭圆几何条件得
的短轴端点和焦点所组成的四边形为正方形,由椭圆几何条件得![]() ,解得
,解得![]() ,
, ![]() (2)联立直线
(2)联立直线![]() 与椭圆方程,利用韦达定理及弦长公式求得
与椭圆方程,利用韦达定理及弦长公式求得![]() ,再利用点到直线距离公式求高,根据三角形面积公式得
,再利用点到直线距离公式求高,根据三角形面积公式得![]() .最后利用基本不等式求最值.
.最后利用基本不等式求最值.
试题解析:解:(Ⅰ)由已知,设椭圆![]() 的方程为
的方程为![]() .
.
∵椭圆![]() 的短轴端点和焦点所组成的四边形为正方形,
的短轴端点和焦点所组成的四边形为正方形,
∴![]() .
.
又![]() ,∴
,∴![]() .
.
由![]() ,得
,得![]() .
.
∴椭圆![]() 的标准方程为
的标准方程为![]() .
.
(Ⅱ)设![]() .
.
联立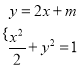 消去
消去![]() ,得
,得![]() .
.
此时有![]() .
.
由一元二次方程根与系数的关系,得
![]() ,
, ![]() .
.
∴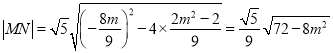 .
.
∵原点![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
∴![]() .
.
由![]() ,得
,得![]() .又
.又![]() ,∴据基本不等式,得
,∴据基本不等式,得
![]() .
.
当且仅当![]() 时,不等式取等号.
时,不等式取等号.
∴![]() 面积的最大值为
面积的最大值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方体ABCD﹣A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=
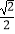 ,给出下列结论:
,给出下列结论:
(1)AC⊥BE;
(2)EF∥平面ABCD;
(3)三棱锥A﹣BEF的体积为定值;
(4)异面直线AE,BF所成的角为定值.
其中错误的结论有( )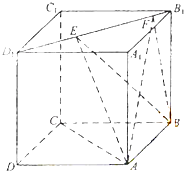
A.0个
B.1 个
C.2个
D.3个 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(Ⅰ)若
 ,求函数
,求函数 的极值;
的极值;(Ⅱ)若
 ,
, ,
, ,使得
,使得 (
( ),求实数
),求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC的内角A、B、C所对的边分别为a,b,c.
(Ⅰ)若a,b,c成等差数列,证明:sinA+sinC=2sin(A+C);
(Ⅱ)若a,b,c成等比数列,且c=2a,求cosB的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】从某企业生产的某中产品中抽取100件,测量这些产品的质量指标值.由测量结果得到如图所示的频率分布直方图,质量指标值落在区间[55,65),[65,75),[75,85]内的频率之比为4:2:1.
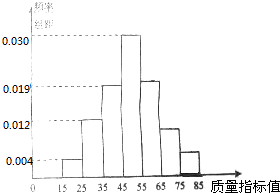
(1)求这些产品质量指标落在区间[75,85]内的概率;
(2)用分层抽样的方法在区间[45,75)内抽取一个容量为6的样本,将该样本看成一个总体,从中任意抽取2件产品,求这2件产品都在区间[45,65)内的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】某食品厂为了检查甲、乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本,并称出它们的重量(单位:克),重量值落在
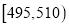 内的产品为合格品,否则为不合格品,统计结果如表:
内的产品为合格品,否则为不合格品,统计结果如表: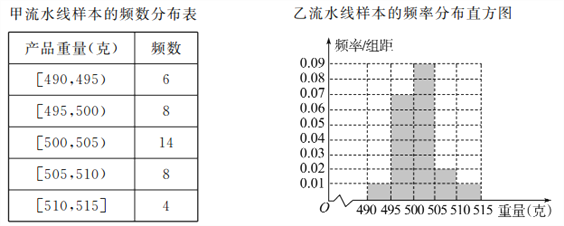
(Ⅰ)求甲流水线样本合格的频率;
(Ⅱ)从乙流水线上重量值落在
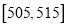 内的产品中任取2个产品,求这2件产品中恰好只有一件合格的概率.
内的产品中任取2个产品,求这2件产品中恰好只有一件合格的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
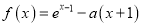 ,
, 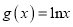 .
.(1)求
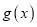 在点
在点 处的切线;
处的切线;(2)讨论
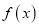 的单调性;
的单调性;(3)当
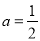 ,
, 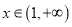 时,求证:
时,求证: 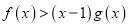 .
.
相关试题

