【题目】△ABC的内角A、B、C所对的边分别为a,b,c.
(Ⅰ)若a,b,c成等差数列,证明:sinA+sinC=2sin(A+C);
(Ⅱ)若a,b,c成等比数列,且c=2a,求cosB的值.
参考答案:
【答案】解:(Ⅰ)∵a,b,c成等差数列,∴a+c=2b,
由正弦定理得:sinA+sinC=2sinB,
∵sinB=sin[π﹣(A+C)]=sin(A+C),
则sinA+sinC=2sin(A+C);
(Ⅱ)∵a,b,c成等比数列,
∴b2=ac,
将c=2a代入得:b2=2a2 , 即b= ![]() a,
a,
∴由余弦定理得:cosB= ![]() =
= ![]() =
= ![]()
【解析】(Ⅰ)由a,b,c成等差数列,利用等差数列的性质得到a+c=2b,再利用正弦定理及诱导公式变形即可得证;(Ⅱ)由a,b,c成等比数列,利用等比数列的性质列出关系式,将c=2a代入表示出b,利用余弦定理表示出cosB,将三边长代入即可求出cosB的值.
【考点精析】关于本题考查的等差数列的通项公式(及其变式)和等差关系的确定,需要了解通项公式:![]() 或
或![]() ;如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,即
;如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,即![]() -
-![]() =d ,(n≥2,n∈N
=d ,(n≥2,n∈N![]() )那么这个数列就叫做等差数列才能得出正确答案.
)那么这个数列就叫做等差数列才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将直线2x﹣y+λ=0沿x轴向左平移1个单位,所得直线与圆x2+y2+2x﹣4y=0相切,则实数λ的值为( )
A.﹣3或7
B.﹣2或8
C.0或10
D.1或11 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方体ABCD﹣A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=
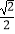 ,给出下列结论:
,给出下列结论:
(1)AC⊥BE;
(2)EF∥平面ABCD;
(3)三棱锥A﹣BEF的体积为定值;
(4)异面直线AE,BF所成的角为定值.
其中错误的结论有( )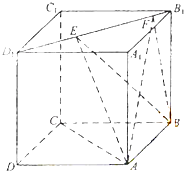
A.0个
B.1 个
C.2个
D.3个 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(Ⅰ)若
 ,求函数
,求函数 的极值;
的极值;(Ⅱ)若
 ,
, ,
, ,使得
,使得 (
( ),求实数
),求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的中心在坐标原点
的中心在坐标原点 ,焦点在
,焦点在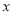 轴上,椭圆
轴上,椭圆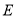 的短轴端点和焦点所组成的四边形为正方形,且椭圆
的短轴端点和焦点所组成的四边形为正方形,且椭圆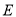 上任意一点到两个焦点的距离之和为
上任意一点到两个焦点的距离之和为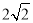 .
.(Ⅰ)求椭圆
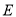 的标准方程;
的标准方程;(Ⅱ)若直线
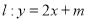 与椭圆
与椭圆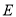 相交于
相交于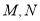 两点,求
两点,求 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】从某企业生产的某中产品中抽取100件,测量这些产品的质量指标值.由测量结果得到如图所示的频率分布直方图,质量指标值落在区间[55,65),[65,75),[75,85]内的频率之比为4:2:1.
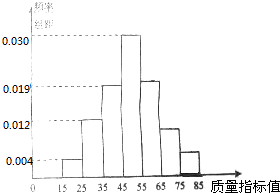
(1)求这些产品质量指标落在区间[75,85]内的概率;
(2)用分层抽样的方法在区间[45,75)内抽取一个容量为6的样本,将该样本看成一个总体,从中任意抽取2件产品,求这2件产品都在区间[45,65)内的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】某食品厂为了检查甲、乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本,并称出它们的重量(单位:克),重量值落在
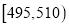 内的产品为合格品,否则为不合格品,统计结果如表:
内的产品为合格品,否则为不合格品,统计结果如表: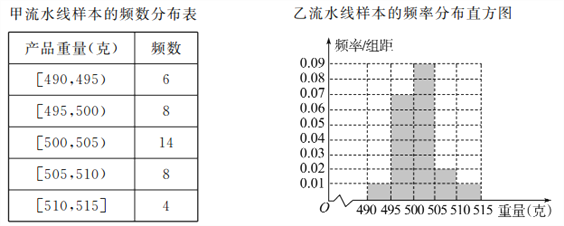
(Ⅰ)求甲流水线样本合格的频率;
(Ⅱ)从乙流水线上重量值落在
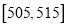 内的产品中任取2个产品,求这2件产品中恰好只有一件合格的概率.
内的产品中任取2个产品,求这2件产品中恰好只有一件合格的概率.
相关试题

