【题目】已知![]() ,
, ![]() .
.
(1)求![]() 在点
在点![]() 处的切线;
处的切线;
(2)讨论![]() 的单调性;
的单调性;
(3)当![]() ,
, ![]() 时,求证:
时,求证: ![]() .
.
参考答案:
【答案】(1)![]() ;(2)见解析;(3)见解析.
;(2)见解析;(3)见解析.
【解析】试题分析:(1)求出原函数的导函数,求出在![]() 处的导数值,即为切线斜率,代入直线方程的点斜式求得切线方程;
处的导数值,即为切线斜率,代入直线方程的点斜式求得切线方程;
(2)求出原函数的导函数,可得当![]() 时导函数在定义域内大于0恒成立,当a<0时求出导函数的零点,由零点对函数的定义域分段,根据导函数在各区间段内的符号得到函数的单调区间;
时导函数在定义域内大于0恒成立,当a<0时求出导函数的零点,由零点对函数的定义域分段,根据导函数在各区间段内的符号得到函数的单调区间;
(3)令![]() ,求其导函数,得到
,求其导函数,得到![]() ,故
,故![]() ,
, ![]() 从而证得答案.
从而证得答案.
试题解析:
(1)![]() ,
,
故![]() 在
在![]() 处的切线为
处的切线为![]() .
.
(2)![]() ;
;
①当![]() 时,
时, ![]() 恒成立,则
恒成立,则![]() 在
在![]() 上单调递增,
上单调递增,
②当![]() 时,
时, ![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
(3)先证明: ![]() 时,
时, ![]() ,
,
令![]() ,
,
则![]() 时,
时, ![]() ,
, ![]() 单调递减,故
单调递减,故![]() ,
,
即![]() .
.
故![]() ,
,
令![]()
则![]() (
(![]() ),
),![]()
而![]() ,
,
故![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
![]() ,
,
由于![]() ,故
,故![]() ,
,
所以![]() 在
在![]() 内恒成立,故
内恒成立,故![]() 在
在![]() 内单调递增,
内单调递增,
![]() ,
,
所以![]() ,
,
故问题得证.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
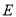 的中心在坐标原点
的中心在坐标原点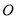 ,焦点在
,焦点在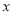 轴上,椭圆
轴上,椭圆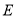 的短轴端点和焦点所组成的四边形为正方形,且椭圆
的短轴端点和焦点所组成的四边形为正方形,且椭圆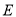 上任意一点到两个焦点的距离之和为
上任意一点到两个焦点的距离之和为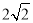 .
.(Ⅰ)求椭圆
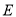 的标准方程;
的标准方程;(Ⅱ)若直线
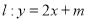 与椭圆
与椭圆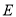 相交于
相交于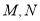 两点,求
两点,求 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】从某企业生产的某中产品中抽取100件,测量这些产品的质量指标值.由测量结果得到如图所示的频率分布直方图,质量指标值落在区间[55,65),[65,75),[75,85]内的频率之比为4:2:1.
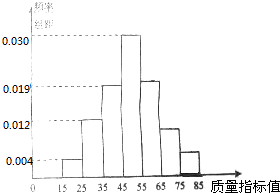
(1)求这些产品质量指标落在区间[75,85]内的概率;
(2)用分层抽样的方法在区间[45,75)内抽取一个容量为6的样本,将该样本看成一个总体,从中任意抽取2件产品,求这2件产品都在区间[45,65)内的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】某食品厂为了检查甲、乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本,并称出它们的重量(单位:克),重量值落在
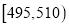 内的产品为合格品,否则为不合格品,统计结果如表:
内的产品为合格品,否则为不合格品,统计结果如表: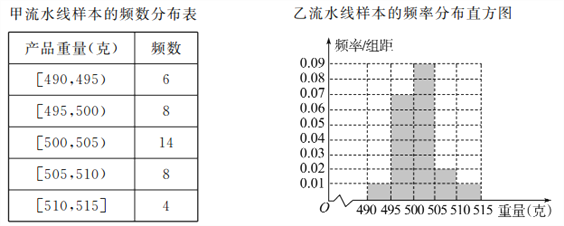
(Ⅰ)求甲流水线样本合格的频率;
(Ⅱ)从乙流水线上重量值落在
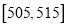 内的产品中任取2个产品,求这2件产品中恰好只有一件合格的概率.
内的产品中任取2个产品,求这2件产品中恰好只有一件合格的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
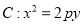 (
(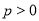 ),过其焦点
),过其焦点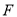 作斜率为1的直线交抛物线
作斜率为1的直线交抛物线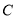 于
于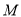 ,
, 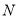 两点,且
两点,且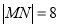 ,
,(1)求抛物线
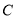 的方程;
的方程;(2)已知动点
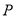 的圆心在抛物线
的圆心在抛物线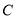 上,且过点
上,且过点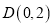 ,若动圆
,若动圆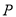 与
与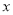 轴交于
轴交于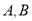 两点,且
两点,且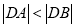 ,求
,求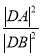 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列{an}满足:a3=3,a5+a7=12,{an}的前n项和为Sn .
(1)求an及Sn;
(2)令bn= (n∈N*),求数列{bn}的前n项和Tn .
(n∈N*),求数列{bn}的前n项和Tn . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点m是直线l:
 x﹣y+3=0与x轴的交点,将直线l绕点m旋转30°,求所得到的直线l′的方程.
x﹣y+3=0与x轴的交点,将直线l绕点m旋转30°,求所得到的直线l′的方程.
相关试题

