【题目】给出定义在![]() 上的两个函数
上的两个函数![]() ,
,![]() .
.
(1)若![]() 在
在![]() 处取最值.求
处取最值.求![]() 的值;
的值;
(2)若函数![]() 在区间
在区间![]() 上单调递减,求实数
上单调递减,求实数![]() 的取值范围;
的取值范围;
(3)试确定函数![]() 的零点个数,并说明理由.
的零点个数,并说明理由.
参考答案:
【答案】(1) ![]() (2)
(2) ![]() (3)两个零点.
(3)两个零点.
【解析】
试题分析:(1) 开区间的最值在极值点取得,因此![]() 在
在![]() 处取极值,即
处取极值,即![]() ,解得
,解得![]() ,需验证(2)
,需验证(2) ![]() 在区间
在区间![]() 上单调递减,转化为
上单调递减,转化为![]() 在区间
在区间![]() 上恒成立,再利用变量分离转化为对应函数最值:
上恒成立,再利用变量分离转化为对应函数最值:![]() 的最大值,根据分式函数求最值方法求得
的最大值,根据分式函数求最值方法求得![]() 最大值2(3)先利用导数研究函数
最大值2(3)先利用导数研究函数![]() 单调性:当
单调性:当![]() 时,递减,当
时,递减,当![]() 时,递增;再考虑区间端点函数值的符号:
时,递增;再考虑区间端点函数值的符号:![]() ,
,
![]() ,
, ![]() ,结合零点存在定理可得零点个数
,结合零点存在定理可得零点个数
试题解析:(1) ![]() 由已知,
由已知,![]() 即:
即: ![]() ,
,
解得:![]() 经检验
经检验 ![]() 满足题意
满足题意
所以 ![]()
(2) ![]()
![]() 要使得
要使得![]() 在区间
在区间![]() 上单调递减,
上单调递减,
则![]() ,即
,即![]() 在区间
在区间![]() 上恒成立
上恒成立
因为![]() ,所以
,所以![]()
设函数![]() ,则
,则![]()
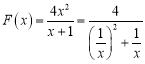
因为![]() ,所以
,所以![]() ,所以
,所以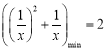
所以![]() ,所以
,所以![]()
(3)函数![]() 有两个零点.因为
有两个零点.因为![]()
所以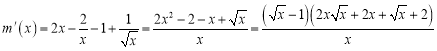
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]()
所以![]() ,
,
![]() ,
,![]()
![]() 故由零点存在理可知:
故由零点存在理可知:
函数![]() 在
在![]() 存在一个零点,函数
存在一个零点,函数![]() 在
在![]() 存在一个零点,
存在一个零点,
所以函数![]() 有两个零点.
有两个零点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
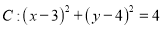 ,直线
,直线 过点
过点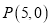 .
.(1)若直线
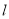 与圆
与圆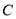 相切,求直线
相切,求直线 的方程;
的方程;(2)若直线
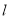 与圆
与圆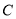 交于
交于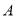 ,
, 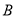 两点,求使得
两点,求使得 面积最大的直线
面积最大的直线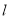 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且acosC+ccosA=2bcosA.
(1)求角A的值;
(2)若 ,
, 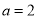 ,求△ABC的面积S.
,求△ABC的面积S. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
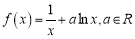 .
.(1) 求函数
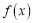 的单调递减区间;
的单调递减区间;(2) 当
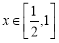 时,
时,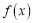 的最小值是
的最小值是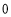 ,求实数
,求实数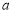 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆N经过点A(3,1),B(﹣1,3),且它的圆心在直线3x﹣y﹣2=0上.
(1)求圆N的方程;
(2)若点D为圆N上任意一点,且点C(3,0),求线段CD的中点M的轨迹方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列
 满足
满足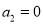 ,
, 
(I)求数列
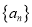 的通项公式;
的通项公式;(II)求数列
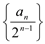 的前n项和.
的前n项和. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,内角A,B,C所对的边分别是a,b,c已知b=4,c=5,A=60°.
(1)求边长a和△ABC的面积;
(2)求sin2B的值.
相关试题

