【题目】已知圆![]() ,直线
,直线![]() 过点
过点![]() .
.
(1)若直线![]() 与圆
与圆![]() 相切,求直线
相切,求直线![]() 的方程;
的方程;
(2)若直线![]() 与圆
与圆![]() 交于
交于![]() ,
, ![]() 两点,求使得
两点,求使得![]() 面积最大的直线
面积最大的直线![]() 的方程.
的方程.
参考答案:
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】试题分析:(1)设直线的方程,根据点到直线的距离等于半径,求出斜率,注意切线斜率不存在的情况; (2)设直线![]() ,由点到直线的距离公式及直线与圆相交时的弦长公式,求出
,由点到直线的距离公式及直线与圆相交时的弦长公式,求出![]() 面积的表达式,由二次函数的最大值,求出斜率
面积的表达式,由二次函数的最大值,求出斜率![]() ,得到直线的方程.
,得到直线的方程.
试题解析:
(1)①当直线![]() 的斜率存在时,设为
的斜率存在时,设为![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,整理得
,整理得![]() .因为直线
.因为直线![]() 与圆
与圆![]() 相切,所以
相切,所以![]() ,解得
,解得![]() ,所以此时直线
,所以此时直线![]() 的方程为
的方程为![]() .
.
②当直线![]() 的斜率不存在时,其方程为
的斜率不存在时,其方程为![]() ,与圆
,与圆![]() 相切,适合题意.
相切,适合题意.
综上,直线![]() 的方程为
的方程为![]() 或
或![]() .
.
(2)由(1)可知当直线![]() 与圆
与圆![]() 相交时,它的斜率一定存在,设其方程为
相交时,它的斜率一定存在,设其方程为![]() .
.
因为圆心到直线![]() 的距离
的距离![]() ,
, ![]() ,所以
,所以![]() 的面积为
的面积为![]()
![]() ,所以当
,所以当![]() 时,
时, ![]() 的面积取得最大值.
的面积取得最大值.
由![]() ,整理得
,整理得![]() ,解得
,解得![]() 或
或![]() .
.
所以直线![]() 的方程为
的方程为![]() 或
或![]() .
.
点睛: 本题主要考查了有关圆的相关知识,属于中档题.思路: (1)由于点(5,0)在圆外,所以过点(5,0)作圆的切线一定有两条,若假设直线的斜率存在,算出来只有一个值,则直线的斜率不存时也符合; (2)三角形的面积用![]() 来表示,开口向下的二次函数在对称轴出取最大值,求出
来表示,开口向下的二次函数在对称轴出取最大值,求出![]() 的值,得到直线的方程.
的值,得到直线的方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=2sinωxcosωx+2
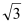 sin2ωx﹣
sin2ωx﹣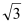 (ω>0)的最小正周期为π.
(ω>0)的最小正周期为π.(1)求函数f(x)的单调增区间;
(2)将函数f(x)的图象向左平移
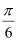 个单位,再向上平移1个单位,得到函数y=g(x)的图象,若y=g(x)在[0,b](b>0)上至少含有10个零点,求b的最小值.
个单位,再向上平移1个单位,得到函数y=g(x)的图象,若y=g(x)在[0,b](b>0)上至少含有10个零点,求b的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
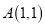 ,
, 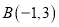 ,点
,点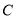 满足
满足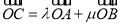 ,其中
,其中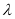 ,
, 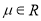 ,且
,且 ;圆
;圆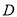 的圆心
的圆心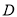 在
在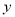 轴上,且与点
轴上,且与点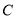 的轨迹相切与点
的轨迹相切与点 .
.(1)求圆
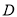 的方程;
的方程;(2)若点
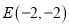 ,点
,点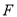 是圆
是圆 上的任意一点,求
上的任意一点,求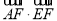 的取值范围;
的取值范围;(3)过点
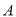 的两条直线分别与圆
的两条直线分别与圆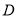 交于
交于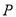 、
、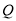 两点,若直线
两点,若直线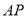 、
、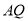 的斜率互为相反数,求证:
的斜率互为相反数,求证: 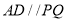 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
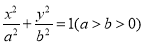 的离心率为
的离心率为 ,椭圆C与y轴交于A、B两点,|AB|=2.
,椭圆C与y轴交于A、B两点,|AB|=2.(Ⅰ)求椭圆C的方程;
(Ⅱ)已知点P是椭圆C上的动点,且直线PA,PB与直线x=4分别交于M、N两点,是否存在点P,使得以MN为直径的圆经过点(2,0)?若存在,求出点P的横坐标;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且acosC+ccosA=2bcosA.
(1)求角A的值;
(2)若 ,
, 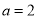 ,求△ABC的面积S.
,求△ABC的面积S. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
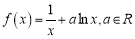 .
.(1) 求函数
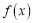 的单调递减区间;
的单调递减区间;(2) 当
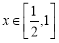 时,
时,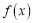 的最小值是
的最小值是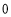 ,求实数
,求实数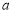 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】给出定义在
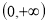 上的两个函数
上的两个函数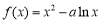 ,
,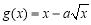 .
. (1)若
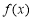 在
在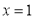 处取最值.求
处取最值.求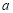 的值;
的值;(2)若函数
 在区间
在区间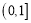 上单调递减,求实数
上单调递减,求实数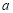 的取值范围;
的取值范围;(3)试确定函数
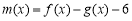 的零点个数,并说明理由.
的零点个数,并说明理由.
相关试题

