【题目】已知圆N经过点A(3,1),B(﹣1,3),且它的圆心在直线3x﹣y﹣2=0上.
(1)求圆N的方程;
(2)若点D为圆N上任意一点,且点C(3,0),求线段CD的中点M的轨迹方程.
参考答案:
【答案】(1)(x﹣2)2+(y﹣4)2=10(2)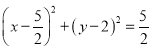
【解析】
试题分析:(1)首先设出方程,将点坐标代入得到关于参数的方程组,通过解方程组得到参数值,从而确定其方程;(2)首先设出点M的坐标,利用中点得到点D坐标,代入圆的方程整理化简得到的中点M的轨迹方程
试题解析:(Ⅰ)由已知可设圆心N(a,3a﹣2),又由已知得|NA|=|NB|, 从而有![]() ,解得:a=2.
,解得:a=2.
于是圆N的圆心N(2,4),半径![]()
所以,圆N的方程为(x﹣2)2+(y﹣4)2=10.(6分)
(2)设M(x,y),D(x1,y1),则由C(3,0)及M为线段CD的中点得: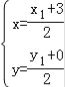 ,解得:
,解得: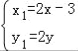 . 又点D在圆N:(x﹣2)2+(y﹣4)2=10上,所以有(2x﹣3﹣2)2+(2y﹣4)2=10,化简得:
. 又点D在圆N:(x﹣2)2+(y﹣4)2=10上,所以有(2x﹣3﹣2)2+(2y﹣4)2=10,化简得:![]()
![]()
故所求的轨迹方程为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且acosC+ccosA=2bcosA.
(1)求角A的值;
(2)若 ,
, 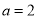 ,求△ABC的面积S.
,求△ABC的面积S. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
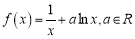 .
.(1) 求函数
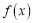 的单调递减区间;
的单调递减区间;(2) 当
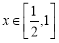 时,
时,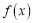 的最小值是
的最小值是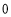 ,求实数
,求实数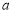 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】给出定义在
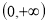 上的两个函数
上的两个函数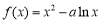 ,
,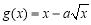 .
. (1)若
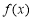 在
在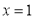 处取最值.求
处取最值.求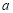 的值;
的值;(2)若函数
 在区间
在区间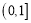 上单调递减,求实数
上单调递减,求实数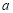 的取值范围;
的取值范围;(3)试确定函数
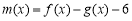 的零点个数,并说明理由.
的零点个数,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列
 满足
满足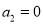 ,
, 
(I)求数列
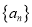 的通项公式;
的通项公式;(II)求数列
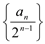 的前n项和.
的前n项和. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,内角A,B,C所对的边分别是a,b,c已知b=4,c=5,A=60°.
(1)求边长a和△ABC的面积;
(2)求sin2B的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在互联网时代,网校培训已经成为青年学习的一种趋势,假设某网校的套题每日的销售量
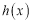 (单位:千套)与销售价格
(单位:千套)与销售价格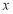 (单位:元/套)满足的关系式
(单位:元/套)满足的关系式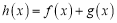 (
(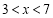 ,
,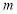 为常数),其中
为常数),其中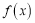 与
与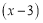 成反比,
成反比,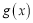 与
与 的平方成正比,已知销售价格为5元/套时,每日可售出套题21千套,销售价格为3.5元/套时,每日可售出套题69千套.
的平方成正比,已知销售价格为5元/套时,每日可售出套题21千套,销售价格为3.5元/套时,每日可售出套题69千套.(1) 求
 的表达式;
的表达式;(2) 假设网校的员工工资,办公等所有开销折合为每套题3元(只考虑销售出的套数),试确定销售价格
 的值,使网校每日销售套题所获得的利润最大.(保留1位小数)
的值,使网校每日销售套题所获得的利润最大.(保留1位小数)
相关试题

