【题目】已知直线 (
(![]() 为参数),曲线
为参数),曲线![]() (
(![]() 为参数).
为参数).
(I)设![]() 与
与![]() 相交于
相交于![]() 两点,求
两点,求![]() ;
;
(II)若把曲线![]() 上各点的横坐标压缩为原来的
上各点的横坐标压缩为原来的![]() 倍,纵坐标压缩为原来的
倍,纵坐标压缩为原来的![]() 倍,得到曲线
倍,得到曲线![]() .设点
.设点![]() 是曲线
是曲线![]() 上的一个动点,求它到直线
上的一个动点,求它到直线![]() 的距离的最小值.
的距离的最小值.
参考答案:
【答案】(I)![]() ;(II)
;(II)![]() .
.
【解析】
试题分析:(I)将直线![]() 化为普通方程,曲线
化为普通方程,曲线![]() 的极坐标方程化为直角坐标方程,联立解方程组求出点
的极坐标方程化为直角坐标方程,联立解方程组求出点![]() 的坐标,利用两点间距离公式求之即可;(II)先求出曲线
的坐标,利用两点间距离公式求之即可;(II)先求出曲线![]() 经过伸缩变换后的参数方程,将点
经过伸缩变换后的参数方程,将点![]() 用曲线的参数方程表示,由点到直线的距离公式和三角恒变换公式即可求距离的最小值.
用曲线的参数方程表示,由点到直线的距离公式和三角恒变换公式即可求距离的最小值.
试题解析: (I)![]() 的普通方程为
的普通方程为![]() ,
,![]() 的普通方程为
的普通方程为![]() .
.
联立方程组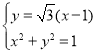 ,解得交点坐标为
,解得交点坐标为![]() ,
,![]() .
.
所以![]() .
.
(II)曲线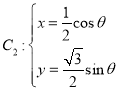 (
(![]() 为参数).
为参数).
设所求的点为![]() ,
,
则![]() 到直线
到直线![]() 的距离
的距离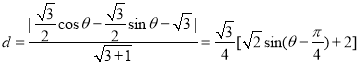 .
.
当![]() 时,取得最小值
时,取得最小值![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的茎叶图记录了甲、乙两组各5名同学的投篮命中次数,乙组记录中有一个数据模糊,无法确认,在图中用
 表示.
表示.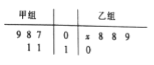
(1)若乙组同学投篮命中次数的平均数比甲组同学的平均数少1,求
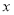 及乙组同学投篮命中次数的方差;
及乙组同学投篮命中次数的方差;(2)在(1)的条件下,分别从甲、乙两组投篮命中次数低于10次的同学中,各随机选取一名,求这两名同学的投篮命中次数之和为16的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆:
 ,点
,点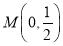 .
.(1)设
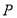 是椭圆
是椭圆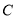 上任意的一点,
上任意的一点,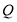 是点
是点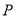 关于坐标原点的对称点,记
关于坐标原点的对称点,记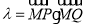 ,求
,求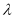 的取值范围;
的取值范围;(2)已知点
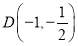 ,
,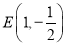 ,
,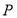 是椭圆
是椭圆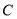 上在第一象限内的点,记
上在第一象限内的点,记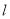 为经过原点与点
为经过原点与点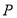 的直线,
的直线,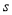 为
为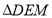 截直线
截直线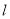 所得的线段长,试将
所得的线段长,试将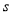 表示成直线
表示成直线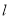 的斜率
的斜率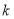 的函数.
的函数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
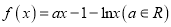 .
.(1)讨论函数
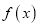 在定义域内的极值点的个数;
在定义域内的极值点的个数;(2)若函数
 在
在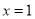 处取得极值,且对
处取得极值,且对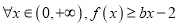 恒成立,求实数
恒成立,求实数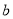 的取值范围;
的取值范围;(3)当
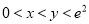 且
且 时,试比较
时,试比较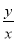 与
与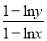 的大小.
的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】记
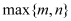 表示
表示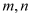 中的最大值,如
中的最大值,如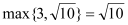 .已知函数
.已知函数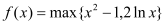 ,
, .
.(1)设
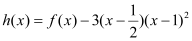 ,求函数
,求函数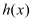 在
在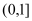 上零点的个数;
上零点的个数; (2)试探究是否存在实数
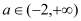 ,使得
,使得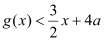 对
对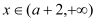 恒成立?若存在,求
恒成立?若存在,求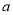 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
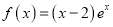 和
和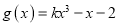 .
.(1)若函数
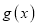 在区间
在区间 不单调,求实数
不单调,求实数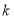 的取值范围;
的取值范围;(2)当
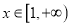 时,不等式
时,不等式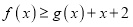 恒成立,求实数
恒成立,求实数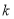 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 上的偶函数,其图象关于点
上的偶函数,其图象关于点 对称,且在区间
对称,且在区间 上是单调函数,则
上是单调函数,则 的值是( )
的值是( )A.
 B.
B.  C.
C.  或
或 D. 无法确定
D. 无法确定
相关试题

