【题目】设![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 是5个正实数(可以相等).
是5个正实数(可以相等).
证明:一定存在4个互不相同的下标![]() ,
, ![]() ,
, ![]() ,
, ![]() ,使得
,使得 .
.
参考答案:
【答案】证明见解析.
【解析】试题分析:可设![]() ,则
,则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 都属于区间
都属于区间![]() ,由抽屉原理知,区间
,由抽屉原理知,区间![]() 或
或![]() 中一定有一个区间至少包含其中的3个数,5个分数的分子、分母的下标特征知,围成的圆圈中,任意相邻两个分数的分子、分母的4个下标互不相同.
中一定有一个区间至少包含其中的3个数,5个分数的分子、分母的下标特征知,围成的圆圈中,任意相邻两个分数的分子、分母的4个下标互不相同. ![]() 、
、![]() 对应的分数的分子、分母的4个下标符合要求.因此,结论成立.
对应的分数的分子、分母的4个下标符合要求.因此,结论成立.
试题解析:不妨设![]() ,考虑以下5个分数:
,考虑以下5个分数: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,①
,①
它们都属于区间![]() .
.
把区间![]() 分成两个区间:
分成两个区间: ![]() 和
和![]() ,由抽屉原理知,区间
,由抽屉原理知,区间![]() 或
或![]() 中一定有一个区间至少包含①中的3个数(记这3个数依次为
中一定有一个区间至少包含①中的3个数(记这3个数依次为![]() ,
, ![]() ,
, ![]() ).
).
将①中的5个数依次围成一个圆圈,则①中任意三个数中都有两个数是相邻的(![]() 与
与![]() 是相邻的),即
是相邻的),即![]() ,
, ![]() ,
, ![]() 中至少有两个数是相邻的.假设
中至少有两个数是相邻的.假设![]() 与
与![]() 相邻,则
相邻,则![]() .
.
另一方面,由①中5个分数的分子、分母的下标特征知,围成的圆圈中,任意相邻两个分数的分子、分母的4个下标互不相同.
于是, ![]() 、
、![]() 对应的分数的分子、分母的4个下标符合要求.因此,结论成立.
对应的分数的分子、分母的4个下标符合要求.因此,结论成立.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于给定的正整数k,若数列{an}满足
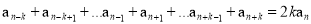
=2kan对任意正整数n(n> k) 总成立,则称数列{an} 是“P(k)数列”.
(1)证明:等差数列{an}是“P(3)数列”;
若数列{an}既是“P(2)数列”,又是“P(3)数列”,证明:{an}是等差数列.
-
科目: 来源: 题型:
查看答案和解析>>【题目】[选修4-4:坐标系与参数方程]在平面坐标系中xOy中,已知直线l的参考方程为
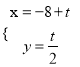 (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为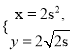 (s为参数)。设p为曲线C上的动点,求点P到直线l的距离的最小值
(s为参数)。设p为曲线C上的动点,求点P到直线l的距离的最小值 -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系中,已知曲线
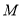 的参数方程为
的参数方程为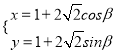 (
(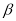 为参数),在极坐标系中,直线
为参数),在极坐标系中,直线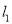 的方程为:
的方程为: 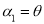 ,直线
,直线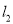 的方程为
的方程为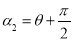 .
.(Ⅰ)写出曲线
 的直角坐标方程,并指出它是何种曲线;
的直角坐标方程,并指出它是何种曲线;(Ⅱ)设
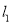 与曲线
与曲线 交于
交于 两点,
两点, 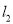 与曲线
与曲线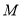 交于
交于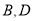 两点,求四边形
两点,求四边形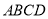 面积的取值范围.
面积的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,设F(x)=x2f(x),则F(x)是( )
,设F(x)=x2f(x),则F(x)是( )
A.奇函数,在(﹣∞,+∞)上单调递减
B.奇函数,在(﹣∞,+∞)上单调递增
C.偶函数,在(﹣∞,0)上递减,在(0,+∞)上递增
D.偶函数,在(﹣∞,0)上递增,在(0,+∞)上递减 -
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=|2x﹣1|,定义f1(x)=x,fn+1(x)=f(fn(x)),已知函数g(x)=fm(x)﹣x有8个零点,则m的值为( )
A.8
B.4
C.3
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】一个化肥厂生产甲种混合肥料1车皮、乙种混合肥料1车皮所需要的主要原料如表:
原料
种类磷酸盐(单位:吨)
硝酸盐(单位:吨)
甲
4
20
乙
2
20
现库存磷酸盐8吨、硝酸盐60吨,计划在此基础上生产若干车皮的甲、乙两种混合肥料.
(1)设x,y分别表示计划生产甲、乙两种肥料的车皮数,试列出x,y满足的数学关系式,并画出相应的平面区域;
(2)若生产1车皮甲种肥料,利润为3万元;生产1车皮乙种肥料,利润为2万元.那么分别生产甲、乙两种肥料多少车皮,能够产生最大利润?最大利润是多少?
相关试题

