【题目】选修4-4:坐标系与参数方程
在直角坐标系中,已知曲线![]() 的参数方程为
的参数方程为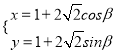 (
(![]() 为参数),在极坐标系中,直线
为参数),在极坐标系中,直线![]() 的方程为:
的方程为: ![]() ,直线
,直线![]() 的方程为
的方程为![]() .
.
(Ⅰ)写出曲线![]() 的直角坐标方程,并指出它是何种曲线;
的直角坐标方程,并指出它是何种曲线;
(Ⅱ)设![]() 与曲线
与曲线![]() 交于
交于![]() 两点,
两点, ![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求四边形
两点,求四边形![]() 面积的取值范围.
面积的取值范围.
参考答案:
【答案】(1) 以![]() 为圆心,
为圆心, ![]() 为半径的圆;(2)
为半径的圆;(2)![]() .
.
【解析】试题分析:(Ⅰ)利用平方法可消去参数,从而可得曲线![]() 的直角坐标方程,进而得它是何种曲线;(Ⅱ)设
的直角坐标方程,进而得它是何种曲线;(Ⅱ)设![]() ,
, ![]() ,曲线
,曲线![]() 的方程化成极坐标方程,将曲线
的方程化成极坐标方程,将曲线![]() 的方程化成极坐标方程得:
的方程化成极坐标方程得: ![]() ,∴
,∴![]() ,
, ![]() ,从而可得结果.
,从而可得结果.
试题解析:(Ⅰ)由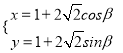 (
(![]() 为参数)消去参数
为参数)消去参数![]() 得:
得: ![]() ,
,
∴曲线![]() 是以
是以![]() 为圆心,
为圆心, ![]() 为半径的圆.
为半径的圆.
(Ⅱ)设![]() ,
, ![]() ,
,
∵![]() 三点共线,则
三点共线,则![]() ①,
①,
将曲线![]() 的方程化成极坐标方程得:
的方程化成极坐标方程得: ![]() ,∴
,∴![]() ,代入①得:
,代入①得: ![]() ,
,
用![]() 代
代![]() 得:
得: ![]()
又∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∵![]() ,∴
,∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】设f(x)是定义在R 且周期为1的函数,在区间
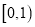 上,
上,  其中集合D=
其中集合D=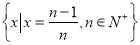 ,则方程f(x)-lgx=0的解的个数是____________
,则方程f(x)-lgx=0的解的个数是____________ -
科目: 来源: 题型:
查看答案和解析>>【题目】对于给定的正整数k,若数列{an}满足
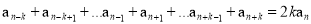
=2kan对任意正整数n(n> k) 总成立,则称数列{an} 是“P(k)数列”.
(1)证明:等差数列{an}是“P(3)数列”;
若数列{an}既是“P(2)数列”,又是“P(3)数列”,证明:{an}是等差数列.
-
科目: 来源: 题型:
查看答案和解析>>【题目】[选修4-4:坐标系与参数方程]在平面坐标系中xOy中,已知直线l的参考方程为
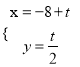 (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为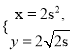 (s为参数)。设p为曲线C上的动点,求点P到直线l的距离的最小值
(s为参数)。设p为曲线C上的动点,求点P到直线l的距离的最小值 -
科目: 来源: 题型:
查看答案和解析>>【题目】设
 ,
,  ,
,  ,
,  ,
,  是5个正实数(可以相等).
是5个正实数(可以相等).证明:一定存在4个互不相同的下标
 ,
,  ,
,  ,
,  ,使得
,使得 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,设F(x)=x2f(x),则F(x)是( )
,设F(x)=x2f(x),则F(x)是( )
A.奇函数,在(﹣∞,+∞)上单调递减
B.奇函数,在(﹣∞,+∞)上单调递增
C.偶函数,在(﹣∞,0)上递减,在(0,+∞)上递增
D.偶函数,在(﹣∞,0)上递增,在(0,+∞)上递减 -
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=|2x﹣1|,定义f1(x)=x,fn+1(x)=f(fn(x)),已知函数g(x)=fm(x)﹣x有8个零点,则m的值为( )
A.8
B.4
C.3
D.2
相关试题

