【题目】设常数![]() 使方程
使方程![]() 在区间
在区间![]() 上恰有三个解
上恰有三个解![]() 且
且![]() ,则实数
,则实数![]() 的值为( )
的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】B
【解析】
解:分别作出y=cosx,x∈(![]() ,3π)与y=m的图象,如图所示,结合图象可得则﹣1<m<0,故排除C,D,再分别令m=﹣
,3π)与y=m的图象,如图所示,结合图象可得则﹣1<m<0,故排除C,D,再分别令m=﹣![]() ,m=﹣
,m=﹣![]() ,求出x1,x2,x3,验证x22=x1x3是否成立;
,求出x1,x2,x3,验证x22=x1x3是否成立;
解:分别作出y=cosx,x∈(![]() ,3π)与y=m的图象,如图所示,方程cosx=m在区间(
,3π)与y=m的图象,如图所示,方程cosx=m在区间(![]() ,3π)上恰有三个解x1,x2,x3(x1<x2<x3),则﹣1<m<0,故排除C,D,
,3π)上恰有三个解x1,x2,x3(x1<x2<x3),则﹣1<m<0,故排除C,D,
当m=﹣![]() 时,此时cosx=﹣
时,此时cosx=﹣![]() 在区间(
在区间(![]() ,3π),
,3π),
解得x1=![]() π,x2=
π,x2=![]() π,x3=
π,x3=![]() π,
π,
则x22=![]() π2≠x1x3=
π2≠x1x3=![]() π2,故A错误,
π2,故A错误,
当m=﹣![]() 时,此时cosx=﹣
时,此时cosx=﹣![]() 在区间(
在区间(![]() ,3π),
,3π),
解得x1=![]() π,x2=
π,x2=![]() π,x3=
π,x3=![]() π,
π,
则x22=![]() π2=x1x3=
π2=x1x3=![]() π2,故B正确,
π2,故B正确,
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 上的焦点为
上的焦点为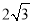 ,离心率为
,离心率为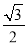 .
.
(1)求椭圆方程;
(2)设过椭圆顶点
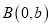 ,斜率为
,斜率为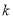 的直线交椭圆于另一点
的直线交椭圆于另一点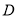 ,交
,交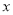 轴于点
轴于点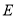 ,且
,且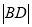 ,
, 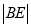 ,
, 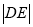 成等比数列,求
成等比数列,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三棱柱
 中,侧面
中,侧面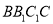 为菱形,
为菱形, 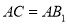 .
.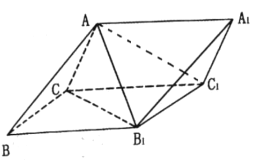
(1)证明:
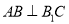 ;
;(2)若
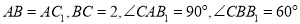 ,求二面角
,求二面角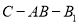 的正弦值.
的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某运输公司有7辆可载
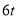 的
的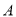 型卡车与4辆可载
型卡车与4辆可载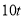 的
的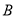 型卡车,有9名驾驶员,建筑某段高速公路中,此公司承包了每天至少搬运
型卡车,有9名驾驶员,建筑某段高速公路中,此公司承包了每天至少搬运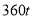 沥青的任务,已知每辆卡车每天往返的次数为
沥青的任务,已知每辆卡车每天往返的次数为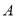 型车8次,
型车8次, 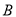 型车6次,每辆卡车每天往返的成本费为
型车6次,每辆卡车每天往返的成本费为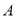 型车160元,
型车160元, 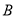 型车252元,每天派出
型车252元,每天派出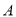 型车和
型车和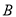 型车各多少辆,公司所花的成本费最低?
型车各多少辆,公司所花的成本费最低? -
科目: 来源: 题型:
查看答案和解析>>【题目】解答
(1)在公比为2的等比数列{an}中,a2与a5的等差中项是9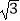 .求a1的值;
.求a1的值;
(2)若函数y=a1sin(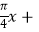 φ),0<φ<π的一部分图象如图所示,M(﹣1,a1),N(3,﹣a1)为图象上的两点,设∠MON=θ,其中O为坐标原点,0<θ<π,求cos(θ﹣φ)的值.
φ),0<φ<π的一部分图象如图所示,M(﹣1,a1),N(3,﹣a1)为图象上的两点,设∠MON=θ,其中O为坐标原点,0<θ<π,求cos(θ﹣φ)的值. 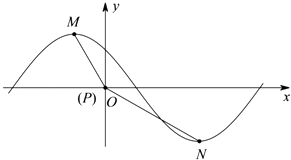
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 为偶函数,且函数
为偶函数,且函数 图象的两相邻对称轴间的距离为
图象的两相邻对称轴间的距离为 .
.(1)求
 的值;
的值;(2)求函数
 的对称轴方程;
的对称轴方程;(3)当
 时,方程
时,方程 有两个不同的实根,求m的取值范围。
有两个不同的实根,求m的取值范围。 -
科目: 来源: 题型:
查看答案和解析>>【题目】设椭圆
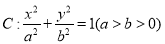 的左焦点为
的左焦点为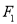 ,右顶点为
,右顶点为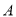 ,离心率为
,离心率为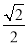 ,已知点
,已知点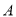 是抛物线
是抛物线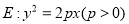 的焦点,点
的焦点,点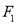 到抛物线准线的距离是
到抛物线准线的距离是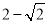 .
.(1)求椭圆
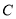 的方程和抛物线
的方程和抛物线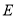 的方程;
的方程;(2)若
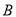 是抛物线
是抛物线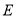 上的一点且在第一象限,满足
上的一点且在第一象限,满足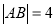 ,直线
,直线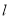 交椭圆于
交椭圆于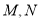 两点,且
两点,且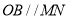 ,当
,当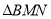 的面积取得最大值时,求直线
的面积取得最大值时,求直线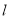 的方程.
的方程.
相关试题

