【题目】设椭圆![]() 的左焦点为
的左焦点为![]() ,右顶点为
,右顶点为![]() ,离心率为
,离心率为![]() ,已知点
,已知点![]() 是抛物线
是抛物线![]() 的焦点,点
的焦点,点![]() 到抛物线准线的距离是
到抛物线准线的距离是![]() .
.
(1)求椭圆![]() 的方程和抛物线
的方程和抛物线![]() 的方程;
的方程;
(2)若![]() 是抛物线
是抛物线![]() 上的一点且在第一象限,满足
上的一点且在第一象限,满足![]() ,直线
,直线![]() 交椭圆于
交椭圆于![]() 两点,且
两点,且![]() ,当
,当![]() 的面积取得最大值时,求直线
的面积取得最大值时,求直线![]() 的方程.
的方程.
参考答案:
【答案】(1)椭圆![]() 的方程为
的方程为![]() ,抛物线
,抛物线![]() 的方程为
的方程为![]() ;(2)
;(2)![]() 或
或![]()
【解析】试题分析:(1)根据椭圆与抛物线几何条件列方程组,解得![]() ,得
,得![]() 即得结果.(2)先根据抛物线定义求出B点坐标,确定MN斜率,设直线方程,与椭圆方程联立,利用韦达定理以及弦长公式得底边边长,根据点到直线距离公式得高,代入三角形面积公式得
即得结果.(2)先根据抛物线定义求出B点坐标,确定MN斜率,设直线方程,与椭圆方程联立,利用韦达定理以及弦长公式得底边边长,根据点到直线距离公式得高,代入三角形面积公式得![]() 的面积函数关系式,最后根据二次函数最值求法确定直线
的面积函数关系式,最后根据二次函数最值求法确定直线![]() 的方程.
的方程.
试题解析:(1)由题意可列方程组:
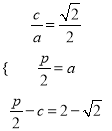 ,解得
,解得![]() ,所以
,所以![]() .
.
从而椭圆![]() 的方程为
的方程为![]() ,抛物线
,抛物线![]() 的方程为
的方程为![]() .
.
(2)可设![]() ,抛物线
,抛物线![]() 的准线方程为
的准线方程为![]() ,
,
由抛物线的定义得: ![]() ,解得
,解得![]() ,
,
所以![]() ,因为点
,因为点![]() 在第一象限,所以
在第一象限,所以![]() .
.
从而![]() .由于
.由于![]() ,所以
,所以![]() ,
,
![]() 的方程可设为:
的方程可设为: ![]() ,即:
,即: ![]() .
.
设![]() ,
,
联立方程组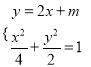 ,消去
,消去![]() 得:
得: ![]() ,
,
可得![]() ,
,
整理为![]() ,解得:
,解得: ![]() .
.
∴![]() ,
, ![]() .
.
所以![]()
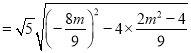
![]()
点![]() 到直线
到直线![]() 的距离
的距离![]() .
.
所以![]()
![]()
![]()
当![]() 时,即:
时,即: ![]() 时
时![]() 的面积取得最大值.
的面积取得最大值.
此时![]() 的方程为
的方程为![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设常数
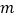 使方程
使方程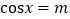 在区间
在区间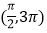 上恰有三个解
上恰有三个解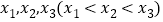 且
且 ,则实数
,则实数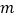 的值为( )
的值为( )A.
 B.
B. 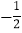 C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】解答
(1)在公比为2的等比数列{an}中,a2与a5的等差中项是9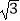 .求a1的值;
.求a1的值;
(2)若函数y=a1sin(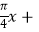 φ),0<φ<π的一部分图象如图所示,M(﹣1,a1),N(3,﹣a1)为图象上的两点,设∠MON=θ,其中O为坐标原点,0<θ<π,求cos(θ﹣φ)的值.
φ),0<φ<π的一部分图象如图所示,M(﹣1,a1),N(3,﹣a1)为图象上的两点,设∠MON=θ,其中O为坐标原点,0<θ<π,求cos(θ﹣φ)的值. 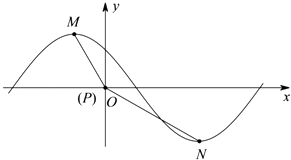
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 为偶函数,且函数
为偶函数,且函数 图象的两相邻对称轴间的距离为
图象的两相邻对称轴间的距离为 .
.(1)求
 的值;
的值;(2)求函数
 的对称轴方程;
的对称轴方程;(3)当
 时,方程
时,方程 有两个不同的实根,求m的取值范围。
有两个不同的实根,求m的取值范围。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
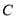 的顶点在坐标原点,焦点在
的顶点在坐标原点,焦点在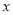 轴上,且过点
轴上,且过点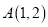 .
.(I)求
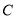 的标准方程;
的标准方程;(Ⅱ)若
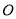 为坐标原点,
为坐标原点, 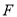 是
是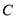 的焦点,过点
的焦点,过点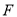 且倾斜角为
且倾斜角为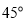 的直线
的直线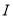 交
交 于
于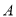 ,
, 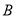 两点,求
两点,求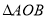 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两所学校高三年级分别有600人,500人,为了解两所学校全体高三年级学生在该地区五校联考的数学成绩情况,采用分层抽样方法从两所学校一共抽取了110名学生的数学成绩,并作出了频数分布统计表如下:
甲校:分组
[70,80)
[80,90)
[90,100)
[100,110)
频数
3
4
7
14
分组
[110,120)
[120,130)
[130,140)
[140,150]
频数
17
x
4
2
乙校:
分组
[70,80)
[80,90)
[90,100)
[100,110)
频数
1
2
8
9
分组
[110,120)
[120,130)
[130,140)
[140,150]
频数
10
10
y
4
(1)计算x,y的值;
(2)若规定考试成绩在[120,150]内为优秀,由以上统计数据填写下面的2×2列联表,并判断是否有90%的把握认为两所学校的数学成绩有差异;
(3)若规定考试成绩在[120,150]内为优秀,现从已抽取的110人中抽取两人,要求每校抽1人,所抽的两人中有人优秀的条件下,求乙校被抽到的同学不是优秀的概率.甲校
乙校
总计
优秀
非优秀
总计
参考公式:K2=
 ,其中n=a+b+c+d.
,其中n=a+b+c+d.
临界值表:P(K2≥k0)
0.10
0.05
0.010
k0
2.706
3.841
6.635
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,AC⊥AB,AD⊥DC,∠DAC=60°,PA=AC=2,AB=1.
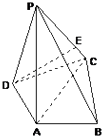
(1)求二面角A﹣PB﹣C的余弦值.
(2)在线段CP上是否存在一点E,使得DE⊥PB,若存在,求线段CE的长度,不存在,说明理由.
相关试题

