【题目】某班学生进行了三次数学测试,第一次有8名学生得满分,第二次有10名学生得满分,第三次有12名学生得满分,已知前两次均为满分的学生有5名,三次测试中至少又一次得满分的学生有15名.若后两次均为满分的学生至多有![]() 名,则
名,则![]() 的值为( )
的值为( )
A. 7 B. 8 C. 9 D. 10
参考答案:
【答案】D
【解析】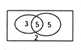
如图,因为三次测试中至少有一次得满分的15名学生的分布情况:
因为第一次有8名学生得满分,第二次有10名学生得满分,前两次均为满分的学生有5名.
所以前两次至少有一次得满分的学生有:8+10-5=13名.又因为三次测试中至少有一次得满分的学生有15名,第三次有12名学生得满分,所以第三次得满分的12名学生中,仅在第三次得满分的学生有2名,其余10名学生则在第一次或第二次得过满分,当第二次得满分的学生最多有10名.故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数f(x)满足f(x+1)﹣f(x)=﹣2x+1且f(2)=15.
(1)求函数f(x)的解析式;
(2)令g(x)=(2﹣2m)x﹣f(x);
①若函数g(x)在x∈[0,2]上是单调函数,求实数m的取值范围;
②求函数g(x)在x∈[0,2]的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=2sin(
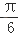 ﹣2x),x∈[0,π])为增函数的区间是( )
﹣2x),x∈[0,π])为增函数的区间是( )
A.[0,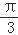 ]
]
B.[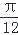 ,
, 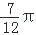 ]
]
C.[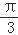 ,
,  ]
]
D.[ ,π]
,π] -
科目: 来源: 题型:
查看答案和解析>>【题目】已知双曲线C1:
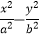 =1,(a>0,b>0)的焦距是实轴长的2倍,若抛物线C2:x2=2py,(p>0)的焦点到双曲线C1的渐近线的距离为2,求抛物线C2的标准方程.
=1,(a>0,b>0)的焦距是实轴长的2倍,若抛物线C2:x2=2py,(p>0)的焦点到双曲线C1的渐近线的距离为2,求抛物线C2的标准方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司研发出一款产品,批量生产前先在某城市销售30天进行市场调查.调查结果发现:日销量
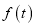 与天数
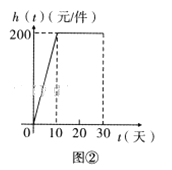
与天数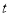 的对应关系服从图①所示的函数关系:每件产品的销售利润
的对应关系服从图①所示的函数关系:每件产品的销售利润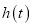 与天数
与天数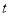 的对应关系服从图②所示的函数关系.图①由抛物线的一部分(
的对应关系服从图②所示的函数关系.图①由抛物线的一部分(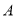 为抛物线顶点)和线段
为抛物线顶点)和线段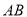 组成.
组成.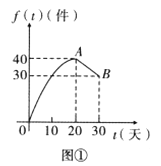
(Ⅰ)设该产品的日销售利润
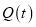
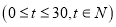 ,分别求出
,分别求出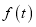 ,
, 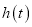 ,
, 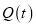 的解析式,
的解析式,(Ⅱ)若在30天的销售中,日销售利润至少有一天超过8500元,则可以投入批量生产,该产品是否可以投入批量生产,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在棱长为3的正方体ABCD﹣A1B1C1D1中,A1E=CF=1.
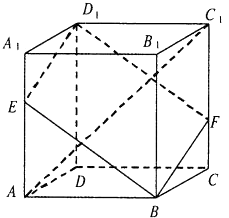
(1)求两条异面直线AC1与D1E所成角的余弦值;
(2)求直线AC1与平面BED1F所成角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
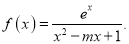
若
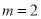 时,求函数
时,求函数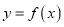 的单调区间;
的单调区间;若
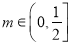 ,则当
,则当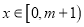 时,函数
时,函数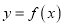 的图像是否总存在直线
的图像是否总存在直线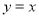 上方?请写出判断过程.
上方?请写出判断过程.
相关试题

