搜索
【题目】已知由实数组成的等比数列{an}的前项和为Sn ， 且满足8a4=a7 ， S7=254．
（1）求数列{an}的通项公式；
（2）对n∈N* ， bn= 
，求数列{bn}的前n项和Tn ．
参考答案：
【答案】
（1）解：设等比数列{an}的公比为q，
由8a4=a7，可得8= 
=q3，解得q=2．
∵S7=254，∴ 
=254，解得a1=2．
∴an=2n
（2）解：bn= 
= 
= 
，
∴Tn= 
+ 
+…+ 
=1﹣ 
【解析】（1）设等比数列{an}的公比为q，由8a4=a7 ， 可得8= =q3 ， 解得q．由S7=254， =254，解得a1 ． （2）bn= = = ，利用“裂项求和”方法即可得出．
-
科目： 来源： 题型：
查看答案和解析>>【题目】一名学生骑自行车上学，从他家到学校的途中有
个交通岗，假设他在各个交通岗遇到红灯的事件是相互独立的，并且概率都是
．求：（
）这名学生在途中遇到
次红灯次数的概率．（
）这名学生在首次停车前经过了
个路口的概率．（
）这名学生至少遇到一次红灯的概率． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知圆C：x2＋y2＋2x－4y＋3＝0.
（1）若圆C的切线在x轴和y轴上的截距相等，求此切线的方程．
（2）点P在直线l：2x－4y＋3＝0上，过点P作圆C的切线，切点记为M，求使|PM|最小的点P的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，在△ABC中，a＝b·cos C＋c·cos B，其中a，b，c分别为角A，B，C的对边，在四面体PABC中，S1，S2，S3，S分别表示△PAB，△PBC，△PCA，△ABC的面积，α，β，γ依次表示面PAB，面PBC，面PCA与底面ABC所成二面角的大小．写出对四面体性质的猜想，并证明你的结论
-
科目： 来源： 题型：
查看答案和解析>>【题目】一个袋中装有
个形状大小完全相同的小球，球的编号分别为
，
，
，
，
，．（
）若从袋中每次随机抽取个球，有放回的抽取次,求取出的两个球编号之和为的概率．（
）若从袋中每次随机抽取个球，有放回的抽取次，求恰有次抽到号球的概率．（
）若一次从袋中随机抽取个球，求球的最大编号为的概率． -
科目： 来源： 题型：
查看答案和解析>>【题目】设y＝f(x)为区间[0,1]上的连续函数，且恒有0≤f(x)≤1，可以用随机模拟方法近似计算积分
.先产生两组(每组N个)区间[0,1]上的均匀随机数x1，x2，…，xN和y1，y2，…，yN，由此得到N个点(xi，yi)(i＝1,2，…，N)．再数出其中满足yi≤f(xi)(i＝1,2，…，N)的点数N1，那么由随机模拟方法可得积分
的近似值为________． -
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，角A，B，C的对边分别为a，b，c，且（c﹣2a）
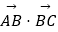=c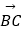 
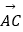
（1）求B的大小；
（2）已知f（x）=cosx（asinx﹣2cosx）+1，若对任意的x∈R，都有f（x）≤f（B），求函数f（x）的单调递减区间．
相关试题
