搜索
【题目】设y＝f(x)为区间[0,1]上的连续函数，且恒有0≤f(x)≤1，可以用随机模拟方法近似计算积分
.先产生两组(每组N个)区间[0,1]上的均匀随机数x1，x2，…，xN和y1，y2，…，yN，由此得到N个点(xi，yi)(i＝1,2，…，N)．再数出其中满足yi≤f(xi)(i＝1,2，…，N)的点数N1，那么由随机模拟方法可得积分
的近似值为________．
参考答案：
【答案】
【解析】因为0≤f(x)≤1且由积分的定义知： 
是由直线x＝0，x＝1及曲线y＝f(x)与x轴所围成的面积，又产生的随机数对在如图所示的正方形内，正方形面积为1，且满足yi≤f(xi)的有N1个点，即在函数f(x)的图象上及图象下方有N1个点，所以用几何概型的概率公式得：f(x)在x＝0到x＝1上与x轴围成的面积为
×1＝
，即
＝
.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，在△ABC中，a＝b·cos C＋c·cos B，其中a，b，c分别为角A，B，C的对边，在四面体PABC中，S1，S2，S3，S分别表示△PAB，△PBC，△PCA，△ABC的面积，α，β，γ依次表示面PAB，面PBC，面PCA与底面ABC所成二面角的大小．写出对四面体性质的猜想，并证明你的结论
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知由实数组成的等比数列{an}的前项和为Sn ， 且满足8a4=a7 ， S7=254．
（1）求数列{an}的通项公式；
（2）对n∈N* ， bn=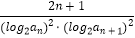
，求数列{bn}的前n项和Tn ． -
科目： 来源： 题型：
查看答案和解析>>【题目】一个袋中装有
个形状大小完全相同的小球，球的编号分别为
，
，
，
，
，．（
）若从袋中每次随机抽取个球，有放回的抽取次,求取出的两个球编号之和为的概率．（
）若从袋中每次随机抽取个球，有放回的抽取次，求恰有次抽到号球的概率．（
）若一次从袋中随机抽取个球，求球的最大编号为的概率． -
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，角A，B，C的对边分别为a，b，c，且（c﹣2a）
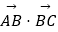=c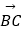 
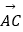
（1）求B的大小；
（2）已知f（x）=cosx（asinx﹣2cosx）+1，若对任意的x∈R，都有f（x）≤f（B），求函数f（x）的单调递减区间． -
科目： 来源： 题型：
查看答案和解析>>【题目】求由直线x＝1、x＝2、y＝0及曲线
围成的图形的面积S. -
科目： 来源： 题型：
查看答案和解析>>【题目】提高过江大桥的车辆通行的车辆通行能力可改善整个城市的交通状况，在一般情况下，大桥上的车流速度
（单位：千米/小时）是车流密度
（单位：辆/千米）的函数．当桥上的车流密度达到200辆/千米时，就会造成堵塞，此时车流速度为0；当
车流密度不超过20辆/千米时，车流速度为60千米/小时．研究表明：当
时，车流速度
是车流密度
的一次函数．（1）当
时，求函数
的表达式；（2）如果车流量（单位时间内通过桥上某观测点的车辆数）
(单位：辆/小时）,那么当车流密度
为多大时，车流量
可以达到最大，并求出最大值．（精确到
辆/小时）.
相关试题
