【题目】为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图如下图,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为a,视力在4.6到5.0之间的学生数为b,则a,b的值分别为 ( )
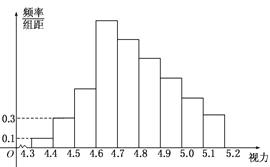
A. 0.27,78 B. 0.27,83 C. 2.7,78 D. 2.7,83
参考答案:
【答案】A
【解析】试题分析:由频率分布直方图知组矩为0.1,4.3~4.4间的频数为100×0.1×0.1=1.4.4~4.5间的频数为100×0.1×0.3=3.又前4组的频数成等比数列,∴公比为3.根据后6组频数成等差数列,且共有100-13=87人.从而4.6~4.7间的频数最大,且为1×33=27,∴a=0.27,设公差为d,则6×27+![]() d=87.∴d=-5,从而b=4×27+
d=87.∴d=-5,从而b=4×27+![]() (-5)=78.故选:A.
(-5)=78.故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若二次函数f(x)=ax2+bx+c的图象顶点坐标为(﹣1,﹣4)且f(0)=﹣3.
(1)求函数f(x)的解析式;
(2)若函数g(x)=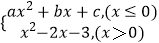 ,画出函数g(x)图象并求单调区间;
,画出函数g(x)图象并求单调区间;
(3)求函数g(x)在[﹣3,2]的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x+
 ,且f(1)=2.
,且f(1)=2.
(1)求m的值;
(2)判断f(x)的奇偶性;
(3)用定义法证明f(x)在区间(1,+∞)上是增函数. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列给出四组函数,表示同一函数的是( )
A.f(x)=x,g(x)=
B.f(x)=2x+1,g(x)=2x﹣1
C.f(x)=x,g(x)=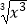
D.f(x)=1,g(x)=x0 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中
①函数f(x)=( )x的递减区间是(﹣∞,+∞);
)x的递减区间是(﹣∞,+∞);
②若函数f(x)=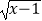 ,则函数定义域是(1,+∞);
,则函数定义域是(1,+∞);
③已知(x,y)在映射f下的象是(x+y,x﹣y),那么(3,1)在映射f下的象是(4,2).
其中正确命题的序号为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x2+1.
(1)判断函数f(x)的奇偶性;
(2)用定义法证明函数f(x)在区间(0,+∞)上是增函数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
. (Ⅰ)若
 ,证明:函数
,证明:函数 是
是 上的减函数;
上的减函数;(Ⅱ)若曲线
 在点
在点 处的切线与直线
处的切线与直线 平行,求
平行,求 的值;
的值;(Ⅲ)若
 ,证明:
,证明:  (其中
(其中 …是自然对数的底数).
…是自然对数的底数).
相关试题

