【题目】若二次函数f(x)=ax2+bx+c的图象顶点坐标为(﹣1,﹣4)且f(0)=﹣3.
(1)求函数f(x)的解析式;
(2)若函数g(x)= ![]() ,画出函数g(x)图象并求单调区间;
,画出函数g(x)图象并求单调区间;
(3)求函数g(x)在[﹣3,2]的值域.
参考答案:
【答案】
(1)解:f(﹣3)=f(1),f(0)=﹣3,
![]() ,
,
∴c=﹣3,b=2,
∴f(x)=x2+2x﹣3,
(2)解:由(1)知,g(x)= ![]() ,
,
由图象可知,函数的单调增区间为(﹣1,0)和(1,+∞),
函数的单调减区间为(﹣∞,﹣1]和[0,1],
(3)解:由图象可知函数g(x)在[﹣3,2]的值域为[﹣4,0]
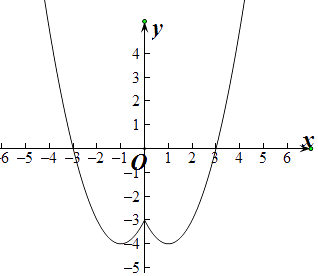
【解析】(1)利用待定系数法即可求出,(2)画图,即可得到函数的单调区间,(3)由图象可知函数的值域.
【考点精析】利用二次函数的性质对题目进行判断即可得到答案,需要熟知当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减.
上递减.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
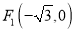 ,
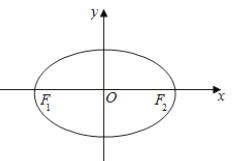
, 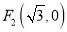 为椭圆
为椭圆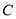 :
:  的左、右焦点,点
的左、右焦点,点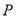 在椭圆
在椭圆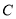 上,且
上,且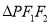 面积的最大值为
面积的最大值为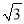 .
.
(Ⅰ)求椭圆
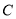 的方程;
的方程;(Ⅱ)若直线
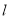 与椭圆
与椭圆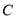 交于
交于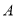 ,
, 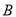 两点,
两点, 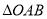 的面积为1,
的面积为1, 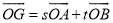 (
( ,
, 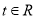 ),当点
),当点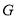 在椭圆
在椭圆 上运动时,试问
上运动时,试问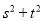 是否为定值?若是定值,求出这个定值;若不是定值,求出
是否为定值?若是定值,求出这个定值;若不是定值,求出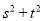 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图所示.

(1)求直方图中x的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为[220,240),[240,260),[260,280),[280,300]的四组用户中,用分层抽样的方法抽取11户居民,则月平均用电量在[220,240)的用户中应抽取多少户?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某机械厂今年进行了五次技能考核,其中甲、乙两名技术骨干得分的平均分相等,成绩统计情况如茎叶图所示(其中
 是0
是0 9的某个整数)
9的某个整数)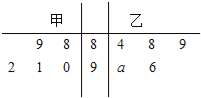
(1)若该厂决定从甲乙两人中选派一人去参加技能培训,从成绩稳定性角度考虑,你认为谁去比较合适?
(2)若从甲的成绩中任取两次成绩作进一步分析,在抽取的两次成绩中,求至少有一次成绩在(90,100]之间的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x+
 ,且f(1)=2.
,且f(1)=2.
(1)求m的值;
(2)判断f(x)的奇偶性;
(3)用定义法证明f(x)在区间(1,+∞)上是增函数. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列给出四组函数,表示同一函数的是( )
A.f(x)=x,g(x)=
B.f(x)=2x+1,g(x)=2x﹣1
C.f(x)=x,g(x)=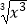
D.f(x)=1,g(x)=x0 -
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图如下图,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为a,视力在4.6到5.0之间的学生数为b,则a,b的值分别为 ( )
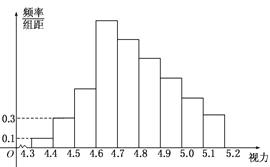
A. 0.27,78 B. 0.27,83 C. 2.7,78 D. 2.7,83
相关试题

