【题目】如图所示的几何体中,四边形ABCD是矩形,平面ABCD⊥平面ABE,已知AB=2,AE=BE=![]() ,且当规定主视图方向垂直平面ABCD时,该几何体的侧视图的面积为
,且当规定主视图方向垂直平面ABCD时,该几何体的侧视图的面积为![]() .若M、N分别是线段DE、CE上的动点,则AM+MN+NB的最小值为________.
.若M、N分别是线段DE、CE上的动点,则AM+MN+NB的最小值为________.

参考答案:
【答案】3
【解析】
试题分析:取AB中点F,∵AE=BE= ![]() ,∴EF⊥AB,
,∴EF⊥AB,
∵平面ABCD⊥平面ABE,∴EF⊥平面ABCD,
易求EF= ![]() ,
,
左视图的面积S= ![]() ADEF=
ADEF= ![]() ×
×![]() AD=
AD= ![]() ,
,
∴AD=1,∴∠AED=∠BEC=30°,∠DEC=60°,
将四棱锥E-ABCD的侧面AED、DEC、CEB展开铺平如图,
则AB2=AE2+BE2-2AEBEcos120°=3+3-2×3×(- ![]() )=9,
)=9,
∴AB=3,
∴AM+MN+BN的最小值为3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
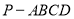 中,
中,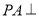 底面
底面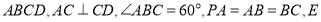 是
是 的中点.
的中点.(1)证明:
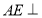 平面
平面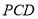 ;
;(2)求
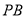 和平面
和平面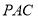 所成的角的正切值.
所成的角的正切值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,P是四边形ABCD所在平面外的一点,四边形ABCD是∠DAB=60°且边长为a的菱形.侧面PAD为正三角形,其所在平面垂直于底面ABCD.

(1)若G为AD边的中点,求证:BG⊥平面PAD;
(2)求证:AD⊥PB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (
( ).
).(1)若函数
 存在极大值和极小值,求
存在极大值和极小值,求 的取值范围;
的取值范围;(2)设
 ,
, 分别为
分别为 的极大值和极小值,若存在实数
的极大值和极小值,若存在实数 ,使得
,使得 ,求
,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
 是平行四边形,
是平行四边形, 平面
平面 ,
, ,
, ,
, ,
, ,
, ,
, ,
, 为
为 的中点.
的中点.
(1)求证:
 平面
平面 ;
;(2)求证:平面
 平面
平面 ;
;(3)求多面体
 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥P-ABCD的底面ABCD为直角梯形,其中BA⊥AD,CD⊥AD,CD=AD=2AB,PA⊥底面ABCD,E是PC的中点.

(1)求证:BE∥平面PAD;
(2)若AP=2AB,求证:BE⊥平面PCD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙三位教师分别在六安一中、二中、一中东校区的三所中学里教不同的学科语文,数学,英语,已知:①甲不在一中工作,乙不在二中工作;②在一中工作的教师不教英语学科;③在二中工作的教师教语文学科;④乙不教数学学科.可以判断乙工作地方和教的学科分别是__________,__________.
相关试题

