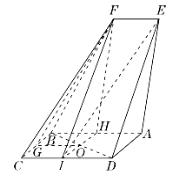
【题目】如图,四边形![]() 是平行四边形,
是平行四边形,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.

(1)求证:![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)求多面体![]() 的体积.
的体积.
参考答案:
【答案】(1)详见解析(2)详见解析(3)![]()
【解析】
试题分析:(1)证明线面平行可证明直线平行于平面内的直线,本题中只需证明![]() ;(2)证明面面垂直可证明其中一个平面经过另外一个平面的垂线,本题中只需证明平面
;(2)证明面面垂直可证明其中一个平面经过另外一个平面的垂线,本题中只需证明平面![]() 中的
中的![]() 平面
平面![]() ;(3)不规则多面体的体积求解时将其分割为柱体和椎体分别求体积
;(3)不规则多面体的体积求解时将其分割为柱体和椎体分别求体积
试题解析:(1)证明:如图,取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,
,
在![]() 中,∵
中,∵![]() 是
是![]() 的中点,
的中点,
∴![]() 且
且![]() ,又∵
,又∵![]() ,∴
,∴![]() 且
且![]() ,即四边形
,即四边形![]() 是平行四边形,∴.又
是平行四边形,∴.又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
(2)证明:在![]() 中,
中,![]() ,取
,取![]() 中点
中点![]() ,连
,连![]() ,∵
,∵![]() ,
,
∴![]() ,又
,又![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() ,又
,又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]()
![]() ,∵
,∵![]() ,
,
∴![]() 平面
平面![]() .又∵
.又∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() .
.
(3)解:连![]() ,并延长交
,并延长交![]() 于
于![]() ,连
,连![]() .
.
∵![]() 分别为
分别为![]() 的中点,∴
的中点,∴![]() ,∴
,∴![]() 是
是![]() 中点,∵
中点,∵![]() ,
,![]() ,
,
∴多面体![]() 为三棱柱,体积为
为三棱柱,体积为![]() ,且四边形
,且四边形![]() 为平行四边形,∴
为平行四边形,∴![]() ,∵
,∵![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,四棱锥
,四棱锥![]() 的体积为
的体积为![]() ,
,
∴多面体![]() 的体积为
的体积为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,P是四边形ABCD所在平面外的一点,四边形ABCD是∠DAB=60°且边长为a的菱形.侧面PAD为正三角形,其所在平面垂直于底面ABCD.

(1)若G为AD边的中点,求证:BG⊥平面PAD;
(2)求证:AD⊥PB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (
( ).
).(1)若函数
 存在极大值和极小值,求
存在极大值和极小值,求 的取值范围;
的取值范围;(2)设
 ,
, 分别为
分别为 的极大值和极小值,若存在实数
的极大值和极小值,若存在实数 ,使得
,使得 ,求
,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的几何体中,四边形ABCD是矩形,平面ABCD⊥平面ABE,已知AB=2,AE=BE=
 ,且当规定主视图方向垂直平面ABCD时,该几何体的侧视图的面积为
,且当规定主视图方向垂直平面ABCD时,该几何体的侧视图的面积为 .若M、N分别是线段DE、CE上的动点,则AM+MN+NB的最小值为________.
.若M、N分别是线段DE、CE上的动点,则AM+MN+NB的最小值为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥P-ABCD的底面ABCD为直角梯形,其中BA⊥AD,CD⊥AD,CD=AD=2AB,PA⊥底面ABCD,E是PC的中点.

(1)求证:BE∥平面PAD;
(2)若AP=2AB,求证:BE⊥平面PCD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙三位教师分别在六安一中、二中、一中东校区的三所中学里教不同的学科语文,数学,英语,已知:①甲不在一中工作,乙不在二中工作;②在一中工作的教师不教英语学科;③在二中工作的教师教语文学科;④乙不教数学学科.可以判断乙工作地方和教的学科分别是__________,__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个四棱锥的三视图如图所示.

(1)求证:PA⊥BD;
(2)在线段PD上是否存在一点Q,使二面角Q-AC-D的平面角为30°?若存在,求
 的值;若不存在,说明理由.
的值;若不存在,说明理由.
相关试题

