【题目】如图,四棱锥P-ABCD的底面ABCD为直角梯形,其中BA⊥AD,CD⊥AD,CD=AD=2AB,PA⊥底面ABCD,E是PC的中点.

(1)求证:BE∥平面PAD;
(2)若AP=2AB,求证:BE⊥平面PCD.
参考答案:
【答案】(1)详见解析(2)详见解析
【解析】
试题分析:(1)欲证BE∥平面PAD,而BE平面EBM,可先证平面EBM∥平面APD,取CD的中点M,连接EM、BM,则四边形ABMD为矩形∴EM∥PD,BM∥AD BM∩EM=M,满足面面平行的判定;(2)取PD的中点F,连接FE,根据线面垂直的判定及性质,及等腰三角形性质,结合线面垂直的判定定理可得AF⊥平面PDC,又由BE∥AF,可得BE⊥平面PDC
试题解析:(1)取PD的中点F,连结AF,FE,
又∵E是PC的中点,
∴在△PDC中,EF∥DC,且EF=![]() ,
,
由条件知AB∥DC,且AB=![]() ,∴ EFAB,
,∴ EFAB,
∴四边形ABEF为平行四边形,∴BE∥AF,
又AF平面PAD,BE平面PAD,∴BE∥平面PAD.
(2)由(1)FE∥DC,BE∥AF,
又∵DC⊥AD,DC⊥PA,∴DC⊥平面PAD,∴DC⊥AF,DC⊥PD,∴EF⊥AF,
在Rt△PAD中,∵AD=AP,F为PD的中点,∴AF⊥PD,
又AF⊥EF且PD∩EF=F,∴AF⊥平面PDC,
又BE∥AF,∴BE⊥平面PDC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (
( ).
).(1)若函数
 存在极大值和极小值,求
存在极大值和极小值,求 的取值范围;
的取值范围;(2)设
 ,
, 分别为
分别为 的极大值和极小值,若存在实数
的极大值和极小值,若存在实数 ,使得
,使得 ,求
,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的几何体中,四边形ABCD是矩形,平面ABCD⊥平面ABE,已知AB=2,AE=BE=
 ,且当规定主视图方向垂直平面ABCD时,该几何体的侧视图的面积为
,且当规定主视图方向垂直平面ABCD时,该几何体的侧视图的面积为 .若M、N分别是线段DE、CE上的动点,则AM+MN+NB的最小值为________.
.若M、N分别是线段DE、CE上的动点,则AM+MN+NB的最小值为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
 是平行四边形,
是平行四边形, 平面
平面 ,
, ,
, ,
, ,
, ,
, ,
, ,
, 为
为 的中点.
的中点.
(1)求证:
 平面
平面 ;
;(2)求证:平面
 平面
平面 ;
;(3)求多面体
 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙三位教师分别在六安一中、二中、一中东校区的三所中学里教不同的学科语文,数学,英语,已知:①甲不在一中工作,乙不在二中工作;②在一中工作的教师不教英语学科;③在二中工作的教师教语文学科;④乙不教数学学科.可以判断乙工作地方和教的学科分别是__________,__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个四棱锥的三视图如图所示.

(1)求证:PA⊥BD;
(2)在线段PD上是否存在一点Q,使二面角Q-AC-D的平面角为30°?若存在,求
 的值;若不存在,说明理由.
的值;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个命题:
①方程
 若有一个正实根,一个负实根,则
若有一个正实根,一个负实根,则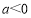 ;
;②函数
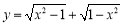 是偶函数,但不是奇函数;
是偶函数,但不是奇函数;③函数
 的值域是
的值域是 ,则函数
,则函数 的值域为
的值域为 ;
;④一条曲线
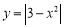 和直线
和直线 的公共点个数是
的公共点个数是 ,则
,则 的值不可能是1.
的值不可能是1.其中正确的有 (写出所有正确的命题的序号).
相关试题

