【题目】在投掷骰子试验中,根据向上的点数可以定义许多事件,如:A={出现1点},B={出现3点或4点},C={出现的点数是奇数},D={出现的点数是偶数}.
(1)说明以上4个事件的关系.
(2)求两两运算的结果.
参考答案:
【答案】(1)见解析;(2)见解析.
【解析】试题分析(1)已知事件![]() 的定义,首先由题意确定骰子向上可能出现的点数以及各个点数的出现能不能同时发生即可确定事件之间的关系;(2)根据互斥事件的加法概率公式对事件
的定义,首先由题意确定骰子向上可能出现的点数以及各个点数的出现能不能同时发生即可确定事件之间的关系;(2)根据互斥事件的加法概率公式对事件![]() 发生的概率进行计算,进而得出最终答案.
发生的概率进行计算,进而得出最终答案.
试题解析:在投掷骰子的试验中,根据向上出现的点数有6种基本事件,
记作Ai={出现的点数为i}(其中i=1,2,…,6).则A=A1,B=A3∪A4,
C=A1∪A3∪A5,D=A2∪A4∪A6.
(1)事件A与事件B互斥,但不对立,事件A包含于事件C,事件A与D互斥,但不对立;事件B与C不是互斥事件,事件B与D也不是互斥事件;事件C与D是互斥事件,也是对立事件.
(2)A∩B=![]() ,A∩C=A,A∩D=
,A∩C=A,A∩D=![]() .
.
A∪B=A1∪A3∪A4={出现的点数为1或3或4},
A∪C=C={出现的点数为1或3或5},
A∪D=A1∪A2∪A4∪A6={出现的点数为1或2或4或6}.
B∩C=A3={出现的点数为3},
B∩D=A4={出现的点数为4}.
B∪C= A1∪A3∪A4∪A5={出现的点数为1或3或4或5}.
B∪D=A2∪A3∪A4∪A6={出现的点数为2或3或4或6}.
C∩D=![]() ,C∪D=A1∪A2∪A3∪A4∪A5∪A6={出现的点数为1,2,3,4,5,6}.
,C∪D=A1∪A2∪A3∪A4∪A5∪A6={出现的点数为1,2,3,4,5,6}.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四棱锥
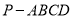 中,
中, 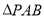 为正三角形,四边形
为正三角形,四边形 为矩形,平面
为矩形,平面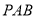
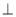 平面
平面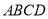 ,
, 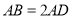 ,
, 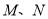 分别为
分别为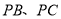 的中点。
的中点。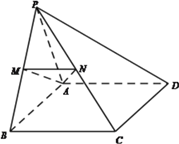
(Ⅰ)求证:
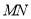 //平面
//平面 ;
;(Ⅱ)求二面角
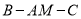 的大小。
的大小。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
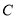 与双曲线
与双曲线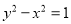 有共同焦点,且离心率为
有共同焦点,且离心率为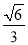 .
.(Ⅰ)求椭圆
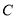 的标准方程;
的标准方程;(Ⅱ)设
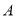 为椭圆
为椭圆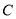 的下顶点,
的下顶点, 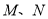 为椭圆上异于
为椭圆上异于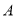 的不同两点,且直线
的不同两点,且直线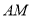 与
与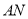 的斜率之积为
的斜率之积为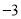 .
.(ⅰ)试问
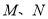 所在直线是否过定点?若是,求出该定点;若不是,请说明理由;
所在直线是否过定点?若是,求出该定点;若不是,请说明理由;(ⅱ)若
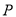 为椭圆
为椭圆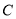 上异于
上异于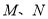 的一点,且
的一点,且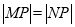 ,求
,求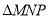 的面积的最小值.
的面积的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校举行汉字听写比赛,为了了解本次比赛成绩情况,从得分不低于50分的试卷中随机抽取100名学生的成绩(得分均为整数,满分100分)进行统计,请根据频率分布表中所提供的数据,解答下列问题:
组号
分组
频数
频率
第1组
[50,60)
5
0.05
第2组
[60,70)
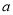
0.35
第3组
[70,80)
30
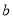
第4组
[80,90)
20
0.20
第5组
[90,100]
10
0.10
合计
100
1.00
(Ⅰ)求
 的值;
的值;(Ⅱ)若从成绩较好的第3、4、5组中按分层抽样的方法抽取6人参加市汉字听写比赛,并从中选出2人做种子选手,求2人中至少有1人是第4组的概率。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场有奖销售中,购满100元商品得1张奖券,多购多得.1 000张奖券为一个开奖单位,设特等奖1个,一等奖10个,二等奖50个.设1张奖券中特等奖、一等奖、二等奖的事件分别为A,B,C,求:
(1)P(A),P(B),P(C).
(2)1张奖券的中奖概率.
(3)1张奖券不中特等奖,且不中一等奖的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
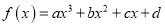 的图象如图所示,则
的图象如图所示,则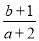 的取值范围是( )
的取值范围是( )
A.
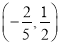 B.
B. 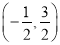 C.
C. 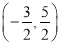 D.
D. 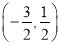
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P是直线x=4上一动点,以P为圆心的圆Γ经定点B(1,0),直线l是圆Γ在点B处的切线,过A(﹣1,0)作圆Γ的两条切线分别与l交于E,F两点.
(1)求证:|EA|+|EB|为定值;
(2)设直线l交直线x=4于点Q,证明:|EB||FQ|=|BF|EQ|.

相关试题

