【题目】设等差数列{an}的前n项和为Sn , 且a2=8,S4=40.数列{bn}的前n项和为Tn , 且Tn﹣2bn+3=0,n∈N* .
(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)设cn=![]() , 求数列{cn}的前n项和Pn .
, 求数列{cn}的前n项和Pn .
参考答案:
【答案】解:(Ⅰ)设等差数列{an}的公差为d,
由题意,得![]() ,
,
解得![]() ,
,
∴an=4n,
∵Tn﹣2bn+3=0,∴当n=1时,b1=3,当n≥2时,Tn﹣1﹣2bn﹣1+3=0,
两式相减,得bn=2bn﹣1 , (n≥2)
则数列{bn}为等比数列,
∴![]() ;
;
(Ⅱ)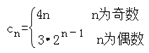 .
.
当n为偶数时,Pn=(a1+a3+…+an﹣1)+(b2+b4+…+bn)
=![]() .
.
当n为奇数时,
(法一)n﹣1为偶数,Pn=Pn﹣1+cn=2(n﹣1)+1+(n﹣1)2﹣2+4n=2n+n2+2n﹣1,
(法二)Pn=(a1+a3+…+an﹣2+an)+(b2+b4+…+bn﹣1)
=![]() .
.
∴![]() .
.
【解析】(Ⅰ)运用等差数列的通项公式与求和公式,根据条件列方程,求出首项和公差,得到通项an , 运用n=1时,b1=T1 , n>1时,bn=Tn﹣Tn﹣1 , 求出bn;
(Ⅱ)写出cn , 然后运用分组求和,一组为等差数列,一组为等比数列,分别应用求和公式化简即可.
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识,掌握数列{an}的前n项和sn与通项an的关系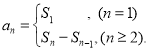 ,以及对等差数列的性质的理解,了解在等差数列{an}中,从第2项起,每一项是它相邻二项的等差中项;相隔等距离的项组成的数列是等差数列.
,以及对等差数列的性质的理解,了解在等差数列{an}中,从第2项起,每一项是它相邻二项的等差中项;相隔等距离的项组成的数列是等差数列.
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列类比推理命题(其中
 为有理数集,
为有理数集, 为实数集,
为实数集,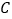 为复数集),其中类比结论正确的是( )
为复数集),其中类比结论正确的是( )A. “若
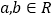 ,则
,则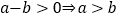 ”类比推出“若
”类比推出“若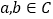 ,则
,则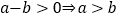 ”.
”.B.
 类比推出
类比推出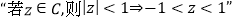
C.
 类比推出
类比推出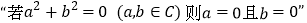
D. “若
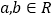 ,则
,则 ”类比推出“若
”类比推出“若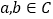 ,则
,则 ”.
”. -
科目: 来源: 题型:
查看答案和解析>>【题目】将5名报名参加运动会的同学分别安排到跳绳、接力,投篮三项比赛中(假设这些比赛都不设人数上限),每人只参加一项,则共有
 种不同的方案;若每项比赛至少要安排一人时,则共有
种不同的方案;若每项比赛至少要安排一人时,则共有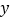 种不同的方案,其中
种不同的方案,其中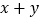 的值为( )
的值为( )A. 543 B. 425 C. 393 D. 275
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥P﹣ABCD中,底面ABCD为菱形,且PA=PD=DA=2,∠BAD=60°
(I)求证:PB⊥AD;
(II)若PB= , 求二面角A﹣PD﹣C的余弦值.
, 求二面角A﹣PD﹣C的余弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某旅游景点预计2013年1月份起前x个月的旅游人数的和p(x)(单位:万人)与x的关系近似地满足p(x)=
 x(x+1)(39﹣2x),(x∈N* , 且x≤12).已知第x月的人均消费额q(x)(单位:元)与x的近似关系是q(x)=
x(x+1)(39﹣2x),(x∈N* , 且x≤12).已知第x月的人均消费额q(x)(单位:元)与x的近似关系是q(x)=
(I)写出2013年第x月的旅游人数f(x)(单位:万人)与x的函数关系式;
(II)试问2013年第几月旅游消费总额最大,最大月旅游消费总额为多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】把数列
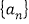 的各项按顺序排列成如下的三角形状,
的各项按顺序排列成如下的三角形状,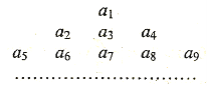
记
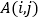 表示第
表示第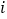 行的第
行的第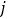 个数,例如
个数,例如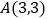 =
=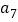 ,若
,若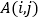 =
=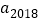 ,则
,则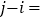 ( )
( )A. 36 B. 37 C. 38 D. 45
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=lnx﹣ax2﹣x(a∈R).
(1)当a=1时,求函数f(x)在(1,﹣2)处的切线方程;
(2)当a≤0时,分析函数f(x)在其定义域内的单调性;
(3)若函数y=g(x)的图象上存在一点P(x0 , y0),使得以P为切点的切线m将图象分割为c1 , c2两部分,且c1 , c2分别完全位于切线m的两侧(除了P点外),则称点x0为函数y=g(x)的“切割点“.问:函数f(x)是否存在满足上述条件的切割点.
相关试题

