【题目】某旅游景点预计2013年1月份起前x个月的旅游人数的和p(x)(单位:万人)与x的关系近似地满足p(x)=![]() x(x+1)(39﹣2x),(x∈N* , 且x≤12).已知第x月的人均消费额q(x)(单位:元)与x的近似关系是q(x)=
x(x+1)(39﹣2x),(x∈N* , 且x≤12).已知第x月的人均消费额q(x)(单位:元)与x的近似关系是q(x)=
(I)写出2013年第x月的旅游人数f(x)(单位:万人)与x的函数关系式;
(II)试问2013年第几月旅游消费总额最大,最大月旅游消费总额为多少元?
参考答案:
【答案】解:(Ⅰ)当x=1时,f(1)=p(1)=37,
当2≤x≤12,且x∈N*时,
f(x)=P(x)﹣P(x﹣1)=![]() x(x+1)(39﹣2x)﹣
x(x+1)(39﹣2x)﹣![]() (x﹣1)x(41﹣2x)=﹣3x2+40x.
(x﹣1)x(41﹣2x)=﹣3x2+40x.
验证x=1符合f(x))=﹣3x2+40x(x∈N* , 且1≤x≤12))
(Ⅱ)第x月旅游消费总额为g(x)= (x∈N*)
(x∈N*)
即g(x)=![]() (x∈N*)
(x∈N*)
当1≤x≤6,且x∈N*时,g′(x)=18x2﹣370x+1400,令g′(x)=0,解得x=5,x=![]() (舍去).
(舍去).
∴当1≤x<5时,g′(x)>0,当5<x≤6时,g′(x)<0,
∴当x=5时,g(x)max=g(5)=3125(万元).
当7≤x≤12,且x∈N*时,g(x)=﹣480x+6400是减函数,∴当x=7时,g(x)max=g(7)=3040(万元),
综上,2013年第5月份的旅游消费总额最大,最大月旅游消费总额为3125万元
【解析】(Ⅰ)根据所给的前x个月旅游人数的和,可以得到第x个月的旅游人数,注意验证第一个月的旅游人数符合表示式.
(Ⅱ)根据所给的表示式,写出第x月旅游消费总额,是一个分段函数,求出分段函数的最大值,把两个最大值进行比较,得到最大月旅游消费总额.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将5名报名参加运动会的同学分别安排到跳绳、接力,投篮三项比赛中(假设这些比赛都不设人数上限),每人只参加一项,则共有
 种不同的方案;若每项比赛至少要安排一人时,则共有
种不同的方案;若每项比赛至少要安排一人时,则共有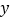 种不同的方案,其中
种不同的方案,其中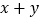 的值为( )
的值为( )A. 543 B. 425 C. 393 D. 275
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥P﹣ABCD中,底面ABCD为菱形,且PA=PD=DA=2,∠BAD=60°
(I)求证:PB⊥AD;
(II)若PB= , 求二面角A﹣PD﹣C的余弦值.
, 求二面角A﹣PD﹣C的余弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设等差数列{an}的前n项和为Sn , 且a2=8,S4=40.数列{bn}的前n项和为Tn , 且Tn﹣2bn+3=0,n∈N* .
(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)设cn= , 求数列{cn}的前n项和Pn .
, 求数列{cn}的前n项和Pn . -
科目: 来源: 题型:
查看答案和解析>>【题目】把数列
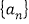 的各项按顺序排列成如下的三角形状,
的各项按顺序排列成如下的三角形状,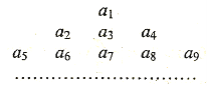
记
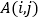 表示第
表示第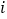 行的第
行的第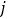 个数,例如
个数,例如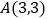 =
=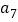 ,若
,若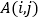 =
=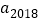 ,则
,则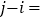 ( )
( )A. 36 B. 37 C. 38 D. 45
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=lnx﹣ax2﹣x(a∈R).
(1)当a=1时,求函数f(x)在(1,﹣2)处的切线方程;
(2)当a≤0时,分析函数f(x)在其定义域内的单调性;
(3)若函数y=g(x)的图象上存在一点P(x0 , y0),使得以P为切点的切线m将图象分割为c1 , c2两部分,且c1 , c2分别完全位于切线m的两侧(除了P点外),则称点x0为函数y=g(x)的“切割点“.问:函数f(x)是否存在满足上述条件的切割点. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 是定义在
是定义在 上的奇函数,且
上的奇函数,且 ,当a,
,当a, ,
, 时,有
时,有 成立.
成立. Ⅰ
Ⅰ 求
求 在区间
在区间 1上的最大值;
1上的最大值; Ⅱ
Ⅱ 若对任意的
若对任意的 都有
都有 ,求实数m的取值范围.
,求实数m的取值范围.
相关试题

