【题目】某中学高三年级有学生500人,其中男生300人,女生200人。为了研究学生的数学成绩是否与性别有关,采用分层抽样的方法,从中抽取了100名学生,统计了他们期中考试的数学分数,然后按照性别分为男、女两组,再将两组的分数分成5组: ![]() 分别加以统计,得到如图所示的频率分布直方图。
分别加以统计,得到如图所示的频率分布直方图。

(I)从样本分数小于110分的学生中随机抽取2人,求两人恰为一男一女的概率;
(II)若规定分数不小于130分的学生为“数学尖子生”,请你根据已知条件完成2×2列联表,并判断是否有90%的把握认为“数学尖子生与性别有关”?
 附表:
附表:
参考答案:
【答案】(Ⅰ)P=![]() ;(Ⅱ)见解析.
;(Ⅱ)见解析.
【解析】试题分析:(1)根据分层抽样原理计算抽取的男、女生人数,利用列举法计算基本事件数,求出对应的概率值;
(2)由频率分布直方图计算对应的数据,填写列联表,计算![]() 值,对照数表即可得出概率结论.
值,对照数表即可得出概率结论.
试题解析:(Ⅰ)由已知得,抽取的100名学生中,男生60名,女生40名,
分数小于等于110分的学生中,男生人有60×0.05=3(人),记为A1,A2,A3;
女生有40×0.05=2(人),记为B1,B2; ………………2分
从中随机抽取2名学生,所有的可能结果共有10种,它们是:
(A1,A2),(A1,A3),(A2,A3),(A1,B1),(A1,B2),
(A2,B1),(A2,B2),(A3,B1),(A3,B2),(B1,B2);
其中,两名学生恰好为一男一女的可能结果共有6种,它们是:
(A1,B1),(A1,B2),(A2,B1),
(A2,B2),(A3,B1),(A3,B2);
故所求的概率为P=![]() .
.
(Ⅱ)由频率分布直方图可知,
在抽取的100名学生中,男生 60×0.25=15(人),女生40×0.375=15(人); …7分
据此可得2×2列联表如下:
数学尖子生 | 非数学尖子生 | 合计 | |
男生 | 15 | 45 | 60 |
女生 | 15 | 25 | 40 |
合计 | 30 | 70 | 100 |
(9分)
所以得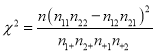
![]() ;
;
因为1.79<2.706,
所以没有90%的把握认为“数学尖子生与性别有关”
-
科目: 来源: 题型:
查看答案和解析>>【题目】设数列{an}的前n项和为Sn , 对任意的正整数n,都有an=5Sn+1成立,记bn=
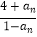 (n∈N*).
(n∈N*).
(1)求数列{an}和数列{bn}的通项公式;
(2)设数列{bn}的前n项和为Rn , 求证:对任意的n∈N* , 都有Rn<4n;
(3)记cn=b2n﹣b2n﹣1(n∈N*),设数列{cn}的前n项和为Tn , 求证:对任意n∈N* , 都有Tn< .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)如图,底面是正三角形的直三棱柱
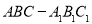 中,D是BC的中点,
中,D是BC的中点, .
.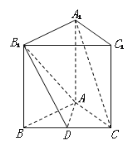
(Ⅰ)求证:
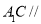 平面
平面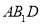 ;
;(Ⅱ)求的A1 到平面
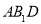 的距离.
的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为加强学生的交通安全教育,对学校旁边
 ,
,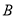 两个路口进行了8天的检测调查,得到每天各路口不按交通规则过马路的学生人数(如茎叶图所示),且
两个路口进行了8天的检测调查,得到每天各路口不按交通规则过马路的学生人数(如茎叶图所示),且 路口数据的平均数比
路口数据的平均数比 路口数据的平均数小2.
路口数据的平均数小2.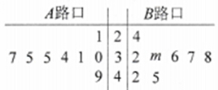
(1)求出
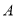 路口8个数据中的中位数和茎叶图中
路口8个数据中的中位数和茎叶图中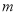 的值;
的值;(2)在
 路口的数据中任取大于35的2个数据,求所抽取的两个数据中至少有一个不小于40的概率.
路口的数据中任取大于35的2个数据,求所抽取的两个数据中至少有一个不小于40的概率. -
科目: 来源: 题型:
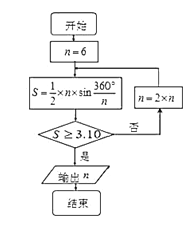
查看答案和解析>>【题目】公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”,利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值
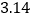 ,这就是著名的“徽率”,如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出
,这就是著名的“徽率”,如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出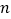 的值为 ( )
的值为 ( )(参考数据:
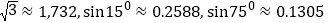 )
)
A.
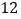 B.
B. 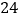 C.
C. 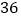 D.
D. 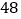
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
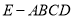 中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=2,DE=3.
中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=2,DE=3.(1)求
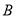 到平面
到平面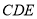 的距离
的距离(2)在线段
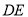 上是否存在一点
上是否存在一点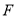 ,使
,使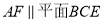 ?若存在,求出
?若存在,求出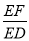 的值;若不存在,说明理由.
的值;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在公务员招聘中,既有笔试又有面试,某单位在2015年公务员考试中随机抽取100名考生的笔试成绩,按成绩分为5组[50,60),[60,70),[70,80),[80,90),[90,100],得到的频率分布直方图如图所示.
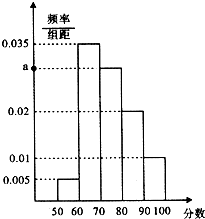
(1)求a值及这100名考生的平均成绩;
(2)若该单位决定在成绩较高的第三、四、五组中按分层抽样抽取6名考生进入第二轮面试,现从这6名考生中抽取3名考生接受单位领导面试,设第四组中恰有1名考生接受领导面试的概率.
相关试题

