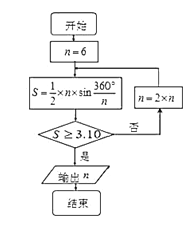
【题目】公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”,利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值![]() ,这就是著名的“徽率”,如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出
,这就是著名的“徽率”,如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出![]() 的值为 ( )
的值为 ( )
(参考数据:![]() )
)
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】B
【解析】
![]() ,故选B.
,故选B.
【点晴】本题主要考查程序框和三角运算,属于较易题型.高考中对于程序框图的考查主要有:输出结果型、完善框图型、确定循环变量取值型、实际应用型等,最常见的题型是以循环结构为主,求解程序框图问题的关键是能够应用算法思想列出并计算每一次循环结果,注意输出值和循环变量以及判断框中的限制条件的关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
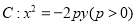 的焦点到准线的距离为
的焦点到准线的距离为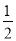 ,直线
,直线 与抛物线
与抛物线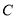 交于
交于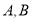 两点,过这两点分别作抛物线
两点,过这两点分别作抛物线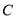 的切线,且这两条切线相交于点
的切线,且这两条切线相交于点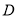 .
.(1)若
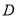 的坐标为
的坐标为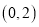 ,求
,求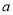 的值;
的值;(2)设线段
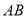 的中点为
的中点为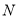 ,点
,点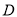 的坐标为
的坐标为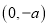 ,过
,过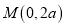 的直线
的直线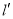 与线段
与线段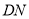 为直径的圆相切,切点为
为直径的圆相切,切点为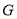 ,且直线
,且直线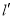 与抛物线
与抛物线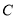 交于
交于 两点,证明:
两点,证明:  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=﹣x2+ax(a∈R).
(1)当a=3时,求函数f(x)在[ ,2]上的最大值和最小值;
,2]上的最大值和最小值;
(2)当函数f(x)在( ,2)单调时,求a的取值范围.
,2)单调时,求a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
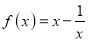 ,
, 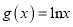 .
.(Ⅰ)求函数
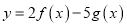 的单调区间;
的单调区间;(Ⅱ)记过函数
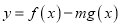 两个极值点
两个极值点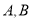 的直线的斜率为
的直线的斜率为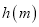 ,问函数
,问函数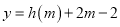 是否存在零点,请说明理由.
是否存在零点,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知以点C(t,
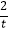 ) (t∈R,t≠0)为圆心的圆与x轴交于点O、A,与y轴交于点O、B,其中O为原点.
) (t∈R,t≠0)为圆心的圆与x轴交于点O、A,与y轴交于点O、B,其中O为原点.
(1)求证:△AOB的面积为定值;
(2)设直线2x+y﹣4=0与圆C交于点M、N,若OM=ON,求圆C的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
 是正四棱柱
是正四棱柱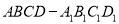 的一个截面,此截面与棱
的一个截面,此截面与棱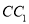 交于点
交于点 ,
, 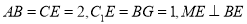 ,其中
,其中 分别为棱
分别为棱 上一点.
上一点.(1)证明:平面
 平面
平面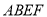 ;
;(2)
 为线段
为线段 上一点,若四面体
上一点,若四面体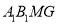 与四棱锥
与四棱锥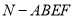 的体积相等,求
的体积相等,求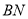 的长.
的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠DAB=90°,∠ADC=135°,AB=5,CD=2
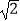 , AD=2,求四边形绕AD旋转一周所围成几何体的表面积及体积.
, AD=2,求四边形绕AD旋转一周所围成几何体的表面积及体积.
相关试题

