【题目】设数列{an}的前n项和为Sn , 对任意的正整数n,都有an=5Sn+1成立,记bn= ![]() (n∈N*).
(n∈N*).
(1)求数列{an}和数列{bn}的通项公式;
(2)设数列{bn}的前n项和为Rn , 求证:对任意的n∈N* , 都有Rn<4n;
(3)记cn=b2n﹣b2n﹣1(n∈N*),设数列{cn}的前n项和为Tn , 求证:对任意n∈N* , 都有Tn< ![]() .
.
参考答案:
【答案】
(1)解:∵an=5Sn+1,
当n=1时,a1=5a1+1,∴a1=﹣ ![]() .
.
当n≥2时,an﹣1=5Sn﹣1+1,
∴an﹣an﹣1=5an,
∴ ![]() =﹣
=﹣ ![]() ,
,
∴{an}是以﹣ ![]() 为首项,以﹣
为首项,以﹣ ![]() 为公比的等比数列.
为公比的等比数列.
∴an=(﹣ ![]() )n.
)n.
∴bn= 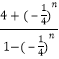 .
.
(2)解:由(1)知bn= 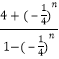 =4+
=4+ ![]() .
.
∴b2k+b2k﹣1=8+ ![]() +
+ ![]() =8+
=8+ ![]() =8﹣
=8﹣ ![]() <8.
<8.
∴当n为偶数时,设n=2m,则Rn=(b1+b2)+(b3+b4)+…+(b2m﹣1+b2m)<8m=4n.
当n为奇数时,设n=2m﹣1,Rn=(b1+b2)+(b3+b4)+…+(b2m﹣3+b2m﹣2)+b2m﹣1<8(m﹣1)+4=4n.
∴对任意的n∈N*,都有Rn<4n.
(3)解:cn=b2n﹣b2n﹣1= ![]() +
+ ![]() =
= ![]() =
= ![]() <
< ![]() =
= ![]() .
.
∵b1=3,b2= ![]() ,∴c1=
,∴c1= ![]() ,
,
∴当n=1时,T1< ![]() .
.
当n≥2时,Tn< ![]() +25(
+25( ![]() +…+
+…+ ![]() )=
)= ![]() +25×
+25× 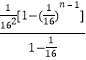
< ![]() +25×
+25× ![]() =
= ![]() .
.
∴对任意n∈N*,都有Tn< ![]() .
.
【解析】(1)利用公式an= ![]() 求出{an}为等比数列,得出其通项公式,代入bn=
求出{an}为等比数列,得出其通项公式,代入bn= ![]() 得出{bn}的通项公式;(2)化简bn , 得出{bn}的相邻两项之和小于8,从而得出结论;(3)化简cn , 得出cn<
得出{bn}的通项公式;(2)化简bn , 得出{bn}的相邻两项之和小于8,从而得出结论;(3)化简cn , 得出cn< ![]() ,从第二项开始使用不等式cn<
,从第二项开始使用不等式cn< ![]() ,得出结论.
,得出结论.
【考点精析】本题主要考查了数列的前n项和和数列的通项公式的相关知识点,需要掌握数列{an}的前n项和sn与通项an的关系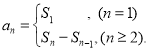 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两人进行两种游戏,两种游戏规则如下:游戏Ⅰ:口袋中有质地、大小完全相同的5个球,编号分别为1,2,3,4,5,甲先摸出一个球,记下编号,放回后乙再摸一个球,记下编号,如果两个编号的和为偶数算甲赢,否则算乙赢.游戏Ⅱ:口袋中有质地、大小完全相同的6个球,其中4个白球,2个红球,由裁判有放回的摸两次球,即第一次摸出记下颜色后放回再摸第二次,摸出两球同色算甲赢,摸出两球不同色算乙赢.
(Ⅰ)求游戏Ⅰ中甲赢的概率;
(Ⅱ)求游戏Ⅱ中乙赢的概率;并比较这两种游戏哪种游戏更公平?试说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】20名同学参加某次数学考试成绩(单位:分)的频率分布直方图如下:
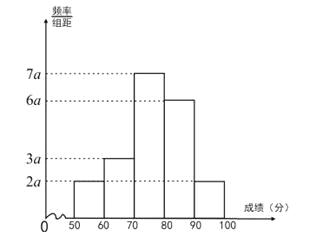
(Ⅰ)求频率分布直方图中
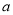 的值;
的值;(Ⅱ)分别求出成绩落在
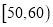 ,
, 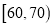 中的学生人数;
中的学生人数;(Ⅲ)从成绩在
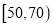 的学生中任选2人,求此2人的成绩都在
的学生中任选2人,求此2人的成绩都在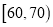 中的概率.
中的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】在三棱锥ABC﹣A1B1C1中,底面ABC是边长为2的正三角形,侧棱AA1⊥底面ABC,AA1=
 ,P、Q分别是AB、AC上的点,且PQ∥BC.
,P、Q分别是AB、AC上的点,且PQ∥BC. 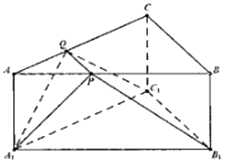
(1)若平面A1PQ与平面A1B1C1相交于直线l,求证:l∥B1C1;
(2)当平面A1PQ⊥平面PQC1B1时,确定点P的位置并说明理由.S. -
科目: 来源: 题型:
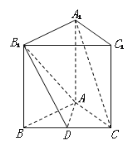
查看答案和解析>>【题目】(12分)如图,底面是正三角形的直三棱柱
 中,D是BC的中点,
中,D是BC的中点, .
.
(Ⅰ)求证:
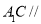 平面
平面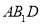 ;
;(Ⅱ)求的A1 到平面
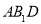 的距离.
的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为加强学生的交通安全教育,对学校旁边
 ,
, 两个路口进行了8天的检测调查,得到每天各路口不按交通规则过马路的学生人数(如茎叶图所示),且
两个路口进行了8天的检测调查,得到每天各路口不按交通规则过马路的学生人数(如茎叶图所示),且 路口数据的平均数比
路口数据的平均数比 路口数据的平均数小2.
路口数据的平均数小2.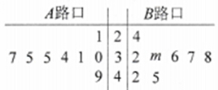
(1)求出
 路口8个数据中的中位数和茎叶图中
路口8个数据中的中位数和茎叶图中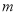 的值;
的值;(2)在
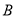 路口的数据中任取大于35的2个数据,求所抽取的两个数据中至少有一个不小于40的概率.
路口的数据中任取大于35的2个数据,求所抽取的两个数据中至少有一个不小于40的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学高三年级有学生500人,其中男生300人,女生200人。为了研究学生的数学成绩是否与性别有关,采用分层抽样的方法,从中抽取了100名学生,统计了他们期中考试的数学分数,然后按照性别分为男、女两组,再将两组的分数分成5组:
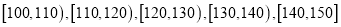 分别加以统计,得到如图所示的频率分布直方图。
分别加以统计,得到如图所示的频率分布直方图。
(I)从样本分数小于110分的学生中随机抽取2人,求两人恰为一男一女的概率;
(II)若规定分数不小于130分的学生为“数学尖子生”,请你根据已知条件完成2×2列联表,并判断是否有90%的把握认为“数学尖子生与性别有关”?
 附表:
附表:
相关试题

