【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,短轴长为
,短轴长为![]() ,右焦点为
,右焦点为![]() (1) 求椭圆
(1) 求椭圆![]() 的标准方程;(2) 若直线
的标准方程;(2) 若直线![]() 经过点
经过点![]() 且与椭圆
且与椭圆![]() 有且仅有一个公共点
有且仅有一个公共点![]() ,过点
,过点![]() 作直线
作直线![]() 交椭圆于另一点
交椭圆于另一点![]() ①证明:当直线
①证明:当直线![]() 与直线
与直线![]() 的斜率
的斜率![]() ,
,![]() 均存在时,
均存在时,![]() .
.![]() 为定值;②求
为定值;②求![]() 面积的最小值。
面积的最小值。
参考答案:
【答案】(1)![]() (2) ①见解析②
(2) ①见解析②![]()
【解析】
(1)根据条件列关于a,b,c的方程组解得a,b,即得结果,(2) ①先设直线![]() 方程:
方程:![]() ,再根据直线与椭圆相切得
,再根据直线与椭圆相切得![]() 关系,并解得P点坐标,最后根据斜率公式计算
关系,并解得P点坐标,最后根据斜率公式计算![]() .
.![]() 为定值,②先确定三角形为直角三角形,再利用弦长公式计算PQ,根据面积公式得函数关系式,最后根据函数单调性确定最小值.
为定值,②先确定三角形为直角三角形,再利用弦长公式计算PQ,根据面积公式得函数关系式,最后根据函数单调性确定最小值.
解:(1)由题意得![]() ,
,
所以椭圆方程为![]()
(2)①证明:由题意知直线![]() 的斜率存在,设直线
的斜率存在,设直线![]() 的方程为
的方程为![]() ,
,
因为点![]() 在直线上,则
在直线上,则![]() ,
,
联立直线与椭圆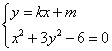 可得
可得![]()
因为直线与椭圆只有一个交点,所以![]() ,即
,即![]() ,
,
由韦达定理得![]() ,
,
又因为![]() 过右焦点
过右焦点![]() ,则
,则![]()
![]()
而![]() ,所以
,所以![]() .
.![]()
②因为F(2,0),所以![]() ,
,![]()
![]() ,所以
,所以![]() ,即
,即![]() ,
,
所以三角形的面积![]() ,
,![]() ,
,
因为![]() ,所以
,所以![]() 方程为
方程为![]() ,设
,设![]()
![]()
与椭圆方程联立 得
得![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,
所以![]()
令![]() ,则
,则![]() ,令
,令![]() ,因此当
,因此当![]()
![]() 时,
时,![]() 面积取最小值
面积取最小值![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系
 中,曲线
中,曲线 的参数方程为
的参数方程为 (
( 为参数,
为参数, ).在以坐标原点为极点
).在以坐标原点为极点 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线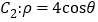
(1)说明
 是哪一种曲线,并将
是哪一种曲线,并将 的方程化为极坐标方程;
的方程化为极坐标方程;(2)直线
 的极坐标方程为
的极坐标方程为 ,其中
,其中 满足
满足 ,若曲线
,若曲线 与
与 的公共点都在
的公共点都在 上,求
上,求 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线C的一个焦点为
 ,对应于这个焦点的准线方程为
,对应于这个焦点的准线方程为
(1)写出抛物线
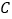 的方程;
的方程;(2)过
 点的直线与曲线
点的直线与曲线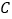 交于
交于 两点,
两点, 点为坐标原点,求
点为坐标原点,求 重心
重心 的轨迹方程;
的轨迹方程;(3)点
 是抛物线
是抛物线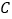 上的动点,过点
上的动点,过点 作圆
作圆 的切线,切点分别是
的切线,切点分别是 .当
.当 点在何处时,
点在何处时, 的值最小?求出
的值最小?求出 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直三棱柱
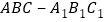 中,
中, ,
, 为
为 的中点,
的中点, ,求证: (1)
,求证: (1)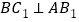 ;
;(2)
 ∥平面
∥平面 。
。
-
科目: 来源: 题型:
查看答案和解析>>【题目】经过中央电视台《魅力中国城》栏目的三轮角逐,黔东南州以三轮竞演总分排名第一名问鼎“最具人气魅力城市”.如图统计了黔东南州从2010年到2017年的旅游总人数(万人次)的变化情况,从一个侧面展示了大美黔东南的魅力所在.根据这个图表,在下列给出的黔东南州从2010年到2017年的旅游总人数的四个判断中,错误的是( )

A. 旅游总人数逐年增加
B. 2017年旅游总人数超过2015、2016两年的旅游总人数的和
C. 年份数与旅游总人数成正相关
D. 从2014年起旅游总人数增长加快
-
科目: 来源: 题型:
查看答案和解析>>【题目】在三棱锥A﹣BCD中,侧棱AB、AC、AD两两垂直,△ABC,△ACD,△ADB的面积分别为
 ,
,  ,
,  , 则三棱锥A﹣BCD的外接球的体积为
, 则三棱锥A﹣BCD的外接球的体积为 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三棱柱
 中,四边形
中,四边形 四边均相等,点
四边均相等,点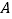 在面
在面 的射影为
的射影为 中点
中点 .
.
(1)证明:
 ;
;(2)若
 ,
, ,
, ,求
,求 点到面
点到面 的距离.
的距离.
相关试题

