【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ).在以坐标原点为极点
).在以坐标原点为极点![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]()
(1)说明![]() 是哪一种曲线,并将
是哪一种曲线,并将![]() 的方程化为极坐标方程;
的方程化为极坐标方程;
(2)直线![]() 的极坐标方程为
的极坐标方程为![]() ,其中
,其中![]() 满足
满足![]() ,若曲线
,若曲线![]() 与
与![]() 的公共点都在
的公共点都在![]() 上,求
上,求![]() .
.
参考答案:
【答案】(1)圆; ρ2-2ρsin θ+1-a2=0.(2) a=1.
【解析】
(1)根据三角函数平方关系消参数得C1的普通方程,再根据x=ρcos θ,y=ρsin θ化为极坐标方程,(2)联立极坐标方程解得16cos2θ-8sin θcos θ+1-a2=0,再根据tan θ=2化简得1-a2=0,解得a=1.
(1)消去参数t得到C1的普通方程为x2+(y-1)2=a2,则C1是以(0,1)为圆心,a为半径的圆.
将x=ρcos θ,y=ρsin θ代入C1的普通方程中,得到C1的极坐标方程为ρ2-2ρsin θ+1-a2=0.
(2)曲线C1,C2的公共点的极坐标满足方程组![]() ,若ρ≠0,由方程组得16cos2θ-8sin θcos θ+1-a2=0,由已知tan θ=2,得16cos2θ-8sin θcos θ=0,从而1-a2=0,解得a=-1(舍去)或a=1.当a=1时,极点也为C1,C2的公共点,且在C3上.所以a=1.
,若ρ≠0,由方程组得16cos2θ-8sin θcos θ+1-a2=0,由已知tan θ=2,得16cos2θ-8sin θcos θ=0,从而1-a2=0,解得a=-1(舍去)或a=1.当a=1时,极点也为C1,C2的公共点,且在C3上.所以a=1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】执行如图所示的程序框图,则输出的k的值为( )

A.4
B.5
C.6
D.7 -
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=
 的图象与函数y=2sinπx(﹣2≤x≤4)的图象所有交点的横坐标之和等于( )
的图象与函数y=2sinπx(﹣2≤x≤4)的图象所有交点的横坐标之和等于( )
A.2
B.4
C.6
D.8 -
科目: 来源: 题型:
查看答案和解析>>【题目】四棱锥
 中,
中,  面
面 ,
,  是平行四边形,
是平行四边形,  ,
, 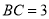 ,点
,点 为棱
为棱 的中点,点
的中点,点 在棱
在棱 上,且
上,且 ,平面
,平面 与
与 交于点
交于点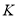 ,则异面直线
,则异面直线 与
与 所成角的正切值为__________.
所成角的正切值为__________.【答案】

【解析】

延长
 交
交 的延长线与点Q,连接QE交PA于点K,设QA=x,
的延长线与点Q,连接QE交PA于点K,设QA=x,由
 ,得
,得 ,则
,则 ,所以
,所以 .
.取
 的中点为M,连接EM,则
的中点为M,连接EM,则 ,
,所以
 ,则
,则 ,所以AK=
,所以AK= .
.由AD//BC,得异面直线
 与
与 所成角即为
所成角即为 ,
,则异面直线
 与
与 所成角的正切值为
所成角的正切值为 .
.【题型】填空题
【结束】
17【题目】在极坐标系中,极点为
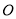 ,已知曲线
,已知曲线 :
:  与曲线
与曲线 :
:  交于不同的两点
交于不同的两点 ,
,  .
.(1)求
 的值;
的值;(2)求过点
 且与直线
且与直线 平行的直线
平行的直线 的极坐标方程.
的极坐标方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线C的一个焦点为
 ,对应于这个焦点的准线方程为
,对应于这个焦点的准线方程为
(1)写出抛物线
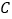 的方程;
的方程;(2)过
 点的直线与曲线
点的直线与曲线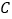 交于
交于 两点,
两点, 点为坐标原点,求
点为坐标原点,求 重心
重心 的轨迹方程;
的轨迹方程;(3)点
 是抛物线
是抛物线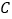 上的动点,过点
上的动点,过点 作圆
作圆 的切线,切点分别是
的切线,切点分别是 .当
.当 点在何处时,
点在何处时, 的值最小?求出
的值最小?求出 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直三棱柱
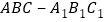 中,
中, ,
, 为
为 的中点,
的中点, ,求证: (1)
,求证: (1)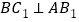 ;
;(2)
 ∥平面
∥平面 。
。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的离心率为
的离心率为 ,短轴长为
,短轴长为 ,右焦点为
,右焦点为 (1) 求椭圆
(1) 求椭圆 的标准方程;(2) 若直线
的标准方程;(2) 若直线 经过点
经过点 且与椭圆
且与椭圆 有且仅有一个公共点
有且仅有一个公共点 ,过点
,过点 作直线
作直线 交椭圆于另一点
交椭圆于另一点 ①证明:当直线
①证明:当直线 与直线
与直线 的斜率
的斜率 ,
, 均存在时,
均存在时, .
. 为定值;②求
为定值;②求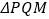 面积的最小值。
面积的最小值。
相关试题

