【题目】如图,已知直三棱柱![]() 中,
中,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() ,求证: (1)
,求证: (1)![]() ;
;
(2)![]() ∥平面
∥平面![]() 。
。

参考答案:
【答案】(1)见解析(2)见解析
【解析】
(1)建立空间直角坐标系,设立各点坐标,利用向量数量积证明线线垂直,(2)建立空间直角坐标系,设立各点坐标,利用向量共线证明线线平行,再根据线面平行判定定理得结果.
证明:如图,以C1点为原点,C1A1,C1B1,C1C所在直线分别为x轴、y轴、z轴建立空间直角坐标系.

设AC=BC=BB1=2,
则A(2,0,2),B(0,2,2),C(0,0,2),A1(2,0,0),B1(0,2,0),C1(0,0,0),D(1,1,2)。
(1)由于![]() =(0,-2,-2),
=(0,-2,-2),![]() =(-2,2,-2),
=(-2,2,-2),
所以![]()
![]() =0-4+4=0,
=0-4+4=0,
因此![]() ⊥
⊥![]() ,故BC1⊥AB1.
,故BC1⊥AB1.
(2)连接A1C,取A1C的中点E,连接DE,由于E(1,0,1),所以![]() =(0,1,1),又
=(0,1,1),又![]() =(0,-2,-2),
=(0,-2,-2),
所以![]() =-
=-![]() ,又ED和BC1不共线,
,又ED和BC1不共线,
所以ED∥BC1,又DE平面CA1D,
BC1平面CA1D,故BC1∥平面CA1D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】四棱锥
 中,
中,  面
面 ,
,  是平行四边形,
是平行四边形,  ,
, 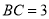 ,点
,点 为棱
为棱 的中点,点
的中点,点 在棱
在棱 上,且
上,且 ,平面
,平面 与
与 交于点
交于点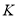 ,则异面直线
,则异面直线 与
与 所成角的正切值为__________.
所成角的正切值为__________.【答案】

【解析】

延长
 交
交 的延长线与点Q,连接QE交PA于点K,设QA=x,
的延长线与点Q,连接QE交PA于点K,设QA=x,由
 ,得
,得 ,则
,则 ,所以
,所以 .
.取
 的中点为M,连接EM,则
的中点为M,连接EM,则 ,
,所以
 ,则
,则 ,所以AK=
,所以AK= .
.由AD//BC,得异面直线
 与
与 所成角即为
所成角即为 ,
,则异面直线
 与
与 所成角的正切值为
所成角的正切值为 .
.【题型】填空题
【结束】
17【题目】在极坐标系中,极点为
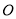 ,已知曲线
,已知曲线 :
:  与曲线
与曲线 :
:  交于不同的两点
交于不同的两点 ,
,  .
.(1)求
 的值;
的值;(2)求过点
 且与直线
且与直线 平行的直线
平行的直线 的极坐标方程.
的极坐标方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系
 中,曲线
中,曲线 的参数方程为
的参数方程为 (
( 为参数,
为参数, ).在以坐标原点为极点
).在以坐标原点为极点 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线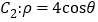
(1)说明
 是哪一种曲线,并将
是哪一种曲线,并将 的方程化为极坐标方程;
的方程化为极坐标方程;(2)直线
 的极坐标方程为
的极坐标方程为 ,其中
,其中 满足
满足 ,若曲线
,若曲线 与
与 的公共点都在
的公共点都在 上,求
上,求 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线C的一个焦点为
 ,对应于这个焦点的准线方程为
,对应于这个焦点的准线方程为
(1)写出抛物线
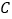 的方程;
的方程;(2)过
 点的直线与曲线
点的直线与曲线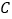 交于
交于 两点,
两点, 点为坐标原点,求
点为坐标原点,求 重心
重心 的轨迹方程;
的轨迹方程;(3)点
 是抛物线
是抛物线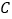 上的动点,过点
上的动点,过点 作圆
作圆 的切线,切点分别是
的切线,切点分别是 .当
.当 点在何处时,
点在何处时, 的值最小?求出
的值最小?求出 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的离心率为
的离心率为 ,短轴长为
,短轴长为 ,右焦点为
,右焦点为 (1) 求椭圆
(1) 求椭圆 的标准方程;(2) 若直线
的标准方程;(2) 若直线 经过点
经过点 且与椭圆
且与椭圆 有且仅有一个公共点
有且仅有一个公共点 ,过点
,过点 作直线
作直线 交椭圆于另一点
交椭圆于另一点 ①证明:当直线
①证明:当直线 与直线
与直线 的斜率
的斜率 ,
, 均存在时,
均存在时, .
. 为定值;②求
为定值;②求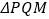 面积的最小值。
面积的最小值。 -
科目: 来源: 题型:
查看答案和解析>>【题目】经过中央电视台《魅力中国城》栏目的三轮角逐,黔东南州以三轮竞演总分排名第一名问鼎“最具人气魅力城市”.如图统计了黔东南州从2010年到2017年的旅游总人数(万人次)的变化情况,从一个侧面展示了大美黔东南的魅力所在.根据这个图表,在下列给出的黔东南州从2010年到2017年的旅游总人数的四个判断中,错误的是( )

A. 旅游总人数逐年增加
B. 2017年旅游总人数超过2015、2016两年的旅游总人数的和
C. 年份数与旅游总人数成正相关
D. 从2014年起旅游总人数增长加快
-
科目: 来源: 题型:
查看答案和解析>>【题目】在三棱锥A﹣BCD中,侧棱AB、AC、AD两两垂直,△ABC,△ACD,△ADB的面积分别为
 ,
,  ,
,  , 则三棱锥A﹣BCD的外接球的体积为
, 则三棱锥A﹣BCD的外接球的体积为
相关试题

