【题目】已知过点A(0,2)的直线![]() 与椭圆C:
与椭圆C:![]() 交于P,Q两点.
交于P,Q两点.
(1)若直线![]() 的斜率为k,求k的取值范围;
的斜率为k,求k的取值范围;
(2)若以PQ为直径的圆经过点E(1,0),求直线![]() 的方程.
的方程.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】
试题(1)由题意设出直线![]() 的方程,联立直线方程与椭圆方程,化为关于
的方程,联立直线方程与椭圆方程,化为关于![]() 的一元二次方程后由判别式大于
的一元二次方程后由判别式大于![]() 求得
求得![]() 的取值范围;(2)设出
的取值范围;(2)设出![]() 的坐标,利用根与系数的关系得到
的坐标,利用根与系数的关系得到![]() 的横坐标的和与积,结合以
的横坐标的和与积,结合以![]() 为直径的圆经过点
为直径的圆经过点![]() ,由
,由![]() 求得
求得![]() 值,则直线
值,则直线![]() 方程可求.
方程可求.
试题解析:(1)依题意,直线![]() 的方程为
的方程为![]() ,由
,由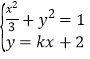 ,消去
,消去![]() 得
得![]() ,令
,令![]() ,解得
,解得![]() 或
或![]() ,所以
,所以![]() 的取值范围是
的取值范围是![]() .
.
(2)当直线![]() 的斜率不存在时,直线
的斜率不存在时,直线![]() 的方程为
的方程为![]() ,则
,则![]() ,此时以
,此时以![]() 为直径的圆过点
为直径的圆过点![]() ,满足题意.直线
,满足题意.直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]()
![]() ,又
,又![]() ,所以
,所以![]() .由(1)知,
.由(1)知,![]() ,所以
,所以
![]()
![]()
![]() .
.
因为以![]() 直径的圆过点
直径的圆过点![]() ,所以
,所以![]() ,即
,即![]() ,解得
,解得![]() ,满足
,满足![]() .
.
故直线![]() 的方程为
的方程为![]() .综上,所求直线
.综上,所求直线![]() 的方程为
的方程为![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】求适合下列条件的圆锥曲线的标准方程:
(1)抛物线的焦点是椭圆
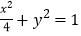 的上顶点;
的上顶点;(2)椭圆的焦距是8,离心率等于
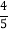 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】过抛物线C:y2=2px(p>0)的焦点F的直线交抛物线于A,B两点,且A,B两点的纵坐标之积为﹣4.
(1)求抛物线C的方程;
(2)已知点D的坐标为(4,0),若过D和B两点的直线交抛物线C的准线于P点,求证:直线AP与x轴交于一定点. -
科目: 来源: 题型:
查看答案和解析>>【题目】在某中学高中某学科竞赛中,该中学100名考生的参赛成绩统计如图所示.

(1)求这100名考生的竞赛平均成绩(同一组中数据用该组区间中点作代表);
(2)记70分以上为优秀,70分及以下为合格,结合频率分布直方图完成下表,并判断是否有99%的把握认为该学科竞赛成绩与性别有关?
合格
优秀
合计
男生
18
女生
25
合计
100
附:
 .
.
0.050
0.010
0.005

3.841
6.635
7.879
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在正方体
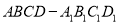 中,点
中,点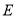 是棱
是棱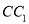 上的一个动点,平面
上的一个动点,平面 交棱
交棱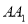 于点
于点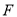 .给出下列命题:
.给出下列命题: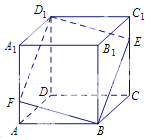
①存在点
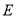 ,使得
,使得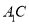 //平面
//平面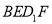 ;
;②对于任意的点
 ,平面
,平面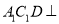 平面
平面 ;
;③存在点
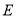 ,使得
,使得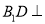 平面
平面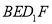 ;
;④对于任意的点
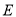 ,四棱锥
,四棱锥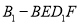 的体积均不变.
的体积均不变.其中正确命题的序号是______.(写出所有正确命题的序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
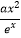 ,直线y=
,直线y= 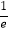 x为曲线y=f(x)的切线(e为自然对数的底数).
x为曲线y=f(x)的切线(e为自然对数的底数).
(1)求实数a的值;
(2)用min{m,n}表示m,n中的最小值,设函数g(x)=min{f(x),x﹣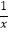 }(x>0),若函数h(x)=g(x)﹣cx2为增函数,求实数c的取值范围.
}(x>0),若函数h(x)=g(x)﹣cx2为增函数,求实数c的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在棱锥
 中,侧面
中,侧面 是边长为2的正三角形,底面
是边长为2的正三角形,底面 是菱形,且
是菱形,且 ,
, 为
为 的中点,二面角
的中点,二面角 为
为 .
.
(1)求证:
 平面
平面 ;
;(2)求二面角
 的大小.
的大小.
相关试题

