【题目】对绵阳南山实验学校的500名教师的年龄进行统计分析,年龄的频率分布直方图如图所示,规定年龄在![]() 内的为青年教师,
内的为青年教师,![]() 内的为中年教师,
内的为中年教师,![]() 内的为老年教师.
内的为老年教师.
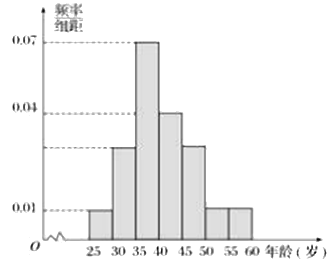
(1)求年龄![]() ,
,![]() 内的教师人数;
内的教师人数;
(2)现用分层抽样的方法从中、青年中抽取18人进行同课异构课堂展示,求抽到年龄在![]() 内的人数.
内的人数.
参考答案:
【答案】(1)75、100 (2)7
【解析】试题分析:(1)本问考查频率分布直方图,根据频率分布直方图的性质可知,每个小矩形的面积等于该组的频率,所有小矩形面积之和为1,![]() 的频率为
的频率为![]() ,该组人数为100人,
,该组人数为100人,![]() 的频率为
的频率为![]() ,该组人数为75人;(2)本问考查分层抽样,根据频率分布直方图可知,中、青年教师人数比例为
,该组人数为75人;(2)本问考查分层抽样,根据频率分布直方图可知,中、青年教师人数比例为![]() ,所以青年教师抽取7人,又因为青年教师
,所以青年教师抽取7人,又因为青年教师![]() 的频率比为
的频率比为![]() ,所以
,所以![]() 内应抽取7人.
内应抽取7人.
试题解析:(1)由正则性可知:直方图面积之和为1
从而可知年龄段在![]() ,
,![]() 面积分别为0.15、0.15.
面积分别为0.15、0.15.
因此年龄段在![]() 的人数为
的人数为![]() ;
;
年龄段![]() 的人数为
的人数为![]() .
.
(2)由分层抽样的原则可知:抽到年龄段在![]() 的人数为:
的人数为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某校高一(1)班全体男生的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分,据此解答如下问题:
(1)求该班全体男生的人数及分数在
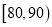 之间的男生人数;
之间的男生人数;(2)根据频率分布直方图,估计该班全体男生的数学平均成绩(同一组中的数据用该组区间的中点值代表);
(3)从分数在
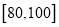 中抽取两个男生,求抽取的两男生分别来自
中抽取两个男生,求抽取的两男生分别来自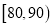 、
、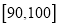 的概率.
的概率.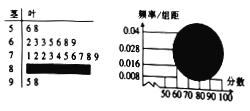
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
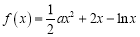 .
.(1)若
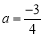 ,判断函数
,判断函数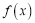 的单调性;
的单调性;(2)若函数
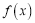 在定义域内单调递减,求实数
在定义域内单调递减,求实数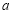 的取值范围;
的取值范围;(3)当
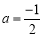 时,关于
时,关于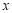 的方程
的方程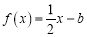 在
在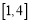 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数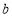 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
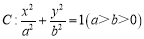 的左、右焦点分别为
的左、右焦点分别为 ,
, ,椭圆上一点
,椭圆上一点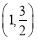 与椭圆右焦点的连线垂直于
与椭圆右焦点的连线垂直于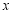 轴.
轴.(1)求椭圆
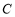 的方程;
的方程;(2)与抛物线
 相切于第一象限的直线
相切于第一象限的直线 ,与椭圆
,与椭圆 交于
交于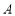 ,
, 两点,与
两点,与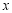 轴交于点
轴交于点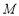 ,线段
,线段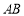 的垂直平分线与
的垂直平分线与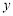 轴交于点
轴交于点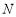 ,求直线
,求直线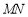 斜率的最小值.
斜率的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】 “一带一路”是“丝绸之路经济带”和“21世纪海上丝绸之路”的简称.某市为了了解人们对“一带一路”的认知程度,对不同年龄和不同职业的人举办了一次“一带一路”知识竞赛,满分100分(90分及以上为认知程度高),现从参赛者中抽取了
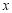 人,按年龄分成5组(第一组:
人,按年龄分成5组(第一组: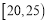 ,第二组
,第二组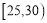 ,第三组:
,第三组: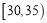 ,第四组:
,第四组: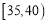 ,第五组:
,第五组: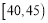 ),得到如图所示的频率分布直方图,已知第一组有6人.
),得到如图所示的频率分布直方图,已知第一组有6人.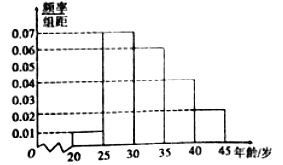
(1)求
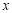 ;
;(2)求抽取的
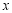 人的年龄的中位数(结果保留整数);
人的年龄的中位数(结果保留整数);(3)从该市大学生、军人、医务人员、工人、个体户五种人中用分层抽样的方法依次抽取6人,42人,36人,24人,12人,分别记为1-5组,从这5个按年龄分的组合5个按职业分的组中每组各选派1人参加知识竞赛代表相应组的成绩,年龄组中1-5组的成绩分别为93,96,97,94,90,职业组中1-5组的成绩分别为93,98,94,95,90.
(i)分别求5个年龄组和5个职业组成绩的平均数和方差;
(ii)以上述数据为依据,评价5个年龄组和5个职业组对“一带一路”的认知程度,并谈谈你的感想.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
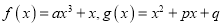 .
.(Ⅰ)若函数
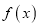 在
在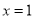 处取得极值,求实数
处取得极值,求实数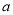 的值;
的值;(Ⅱ)在(Ⅰ)的条件下,函数
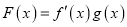 (其中
(其中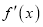 为函数
为函数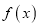 的导数)的图像关于直线
的导数)的图像关于直线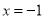 对称,求函数
对称,求函数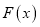 单调区间;
单调区间;(Ⅲ)在(Ⅱ)的条件下,若对任意的
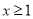 ,都有
,都有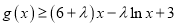 恒成立,求实数
恒成立,求实数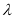 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,设P是圆
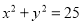 上的动点,点D是P在x轴上的投影,M为线段PD上一点,且
上的动点,点D是P在x轴上的投影,M为线段PD上一点,且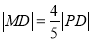 ,
,(1)当P在圆上运动时,求点M的轨迹C的方程;
(2)求过点(3,0)且斜率为
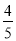 的直线被轨迹C所截线段的长度.
的直线被轨迹C所截线段的长度.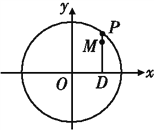
相关试题

