【题目】设函数f(x)=ax2-lnx。
(Ⅰ)当a=![]() 时,判断f(x)的单调性;(Ⅱ)设f(x)≤x3+4x-lnx,在定义域内恒成立,求a的取值范围。
时,判断f(x)的单调性;(Ⅱ)设f(x)≤x3+4x-lnx,在定义域内恒成立,求a的取值范围。
参考答案:
【答案】(1)f(x)在0<x≤1上,函数为减函数;在x>1上,函数为增函数;(2)a≤4.
【解析】试题分析:(1)将条件带入求导,得![]() =x-
=x-![]() ,进而根据导数的正负可得函数的单调性;
,进而根据导数的正负可得函数的单调性;
(2)令H(x)= f(x)-(x3+4x-lnx)= -x3+![]() x2-4x=x(-x2+ax-4)所以要使f(x)≤x3+4x-lnx,在定义域内恒成立,只需H(x)≤0,在定义域内恒成立,即x(-x2+ax-4) ≤0在x>0上恒成立,进而转化为-x2+ax-4≤0在x>0上恒成立,进而可得解.
x2-4x=x(-x2+ax-4)所以要使f(x)≤x3+4x-lnx,在定义域内恒成立,只需H(x)≤0,在定义域内恒成立,即x(-x2+ax-4) ≤0在x>0上恒成立,进而转化为-x2+ax-4≤0在x>0上恒成立,进而可得解.
试题解析:
(1)、当a=![]() 时,f(x)=
时,f(x)=![]() x2-lnx,
x2-lnx, ![]() =x-
=x-![]()
令导函数等于0,解得x=1或x=-1(舍),
所以当![]() >0时,x>1,当
>0时,x>1,当![]() <0,0<x<1
<0,0<x<1
所以f(x)在0<x≤1上,函数为减函数;在x>1上,函数为增函数。
(2)令H(x)= f(x)-(x3+4x-lnx)= -x3+![]() x2-4x=x(-x2+ax-4)
x2-4x=x(-x2+ax-4)
所以要使f(x)≤x3+4x-lnx,在定义域内恒成立,只需H(x)≤0,在定义域内恒成立,
即x(-x2+ax-4) ≤0在x>0上恒成立。
由于x>0,所以只要-x2+ax-4≤0在x>0上恒成立
所以应满足△≤0或者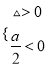 ,所以a≤4.
,所以a≤4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
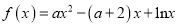 .
.(1)当
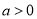 时,若
时,若 在区间
在区间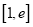 上的最小值为
上的最小值为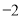 ,求
,求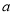 的取值范围;
的取值范围;(2)若对任意
 ,
, 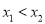 ,且
,且 恒成立,求
恒成立,求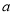 的取值范围.
的取值范围. -
科目: 来源: 题型:
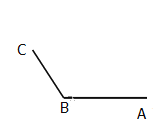
查看答案和解析>>【题目】如图所示,A , B , C是三个观察站,A在B的正东,两地相距6km,C在B的北偏西30°,两地相距4km,在某一时刻,A观察站发现某种信号,并知道该信号的传播速度为1km/s,4s后B , C两个观察站同时发现这种信号,在以过A , B两点的直线为x轴,以AB的垂直平分线为y轴建立的平面直角坐标系中,指出发出这种信号的P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】由大于0的自然数构成的等差数列{an},它的最大项为26,其所有项的和为70;
(1)求数列{an}的项数n;
(2)求此数列. -
科目: 来源: 题型:
查看答案和解析>>【题目】由大于0的自然数构成的等差数列{an},它的最大项为26,其所有项的和为70;
(1)求数列{an}的项数n;
(2)求此数列. -
科目: 来源: 题型:
查看答案和解析>>【题目】近几年出现各种食品问题,食品添加剂会引起血脂增高、血压增高、血糖增高等疾病.为了解三高疾病是否与性别有关,医院随机对入院的60人进行了问卷调查,得到了如下的列联表:
患三高疾病
不患三高疾病
合计
男
6
30
女
合计
36
下面的临界值表供参考:

0.15
0.10
0.05
0.025
0.010
0.005
0.001
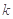
2.072
2.706
3.841
5.024
6.635
7.879
10.828
(参考公式
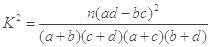 ,其中
,其中 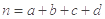 )
)
(1)请将如图的列联表补充完整;若用分层抽样的方法在患三高疾病的人群中抽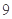 人,其中女性抽多少人?
人,其中女性抽多少人?
(2)为了研究三高疾病是否与性别有关,请计算出统计量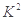 ,并说明你有多大的把握认为三高疾病与性别有关?
,并说明你有多大的把握认为三高疾病与性别有关? -
科目: 来源: 题型:
查看答案和解析>>【题目】一列火车从重庆驶往北京,沿途有n个车站(包括起点站重庆和终点站北京).车上有一邮政车厢,每停靠一站便要卸下火车已经过的各站发往该站的邮袋各1个,同时又要装上该站发往以后各站的邮袋各1个,设从第k站出发时,邮政车厢内共有邮袋ak个(k=1,2,…,n).
(1)求数列{ak}的通项公式;
(2)当k为何值时,ak的值最大,求出ak的最大值.
相关试题

