【题目】已知函数f(x)= ![]() (m,n∈R)在x=1处取得极值2.
(m,n∈R)在x=1处取得极值2.
(1)求f(x)的解析式;
(2)k为何值时,方程f(x)﹣k=0只有1个根
(3)设函数g(x)=x2﹣2ax+a,若对于任意x1∈R,总存在x2∈[﹣1,0],使得g(x2)≤f(x1),求a的取值范围.
参考答案:
【答案】
(1)解:因为函数f(1)= ![]() .
.
所以m=2+2n,f(x)= ![]() ,
,
又f(x)在x=1处取得极值,
f  =
= ![]() ,
,
f ![]() ,n=1,则m=4,
,n=1,则m=4,
经检验满足题意,
所以 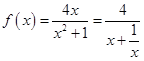 ;
;
(2)解:由f(x)﹣k=0,得k=f(x),
由(1)得f ![]() ,
,
令f′(x)=0,得x=±1.
当x变化时,f′(x),f(x)的变化情况如下表:
x | (﹣∞,﹣1) | ﹣1 | (﹣1,1) | 1 | (1,+∞) |
f'(x) | ﹣ | 0 | + | 0 | ﹣ |
f(x) | 单调递减 | 极小值 | 单调递增 | 极大值 | 单调递减 |
所以f(x)在x=﹣1处取得极小值﹣2,在x=1处取得极大值2
又 ![]() 如图
如图
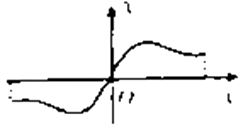
所以k=±2或0时,方程有一个根
(3)解:对于任意x1∈R,总存在x2∈[﹣1,0],使得g(x2)≤f(x1),
只需g(x2)min≤f(x1)min,
即当x∈[﹣1,0]时,x2﹣2ax+a≤﹣2恒成立
只需 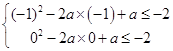 ,
,
解得a≤﹣2
a的取值范围为a≤﹣2
【解析】(1)函数f(1)= ![]() .所以m=2+2n,f(x)=
.所以m=2+2n,f(x)= ![]() ,又f(x)在x=1处取得极值,f
,又f(x)在x=1处取得极值,f ![]() ,n=1,则m=4(2)由f(x)﹣k=0,得k=f(x),由(1)得f
,n=1,则m=4(2)由f(x)﹣k=0,得k=f(x),由(1)得f ![]() ,令f′(x)=0,得x=±1.求出单调区间,根据图象即可求解.(3)对于任意x1∈R,总存在x2∈[﹣1,0],使得g(x2)≤f(x1),只需g(x2)min≤f(x1)min,即当x∈[﹣1,0]时,x2﹣2ax+a≤﹣2恒成立,只需
,令f′(x)=0,得x=±1.求出单调区间,根据图象即可求解.(3)对于任意x1∈R,总存在x2∈[﹣1,0],使得g(x2)≤f(x1),只需g(x2)min≤f(x1)min,即当x∈[﹣1,0]时,x2﹣2ax+a≤﹣2恒成立,只需 ![]() ,解得a.
,解得a.
【考点精析】本题主要考查了函数的极值与导数的相关知识点,需要掌握求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值才能正确解答此题.
是极小值才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P-ABCD中,AB//CD,且


(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC,
 ,且四棱锥P-ABCD的体积为
,且四棱锥P-ABCD的体积为 ,求该四棱锥的侧面积.
,求该四棱锥的侧面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=lnx,g(x)=0.5x2﹣bx,(b为常数).
(1)函数f(x)的图象在点(1,f(1))处的切线与函数g(x)的图象相切,求实数b的值;
(2)若函数h(x)=f(x)+g(x)在定义域上不单调,求实数b的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数
 的图象与
的图象与 轴交于点
轴交于点 ,周期是
,周期是 .
.(1)求函数解析式,并写出函数图象的对称轴方程和对称中心;
(2)已知点
 ,点
,点 是该函数图象上一点,点
是该函数图象上一点,点 是
是 的中点,当
的中点,当 ,
,  时,求
时,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
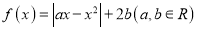 .
.(1)当
 时,解方程
时,解方程 ;
; (2)当
 时,若不等式
时,若不等式 在
在 上恒成立,求实数a的取值范围;
上恒成立,求实数a的取值范围;(3)若a为常数,且函数
 在区间
在区间 上存在零点,求实数b的取值范围.
上存在零点,求实数b的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.

根据该折线图,下列结论错误的是( )
A. 月接待游客量逐月增加
B. 年接待游客量逐年增加
C. 各年的月接待游客量高峰期大致在7,8月
D. 各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
-
科目: 来源: 题型:
查看答案和解析>>【题目】在极坐标系下,已知曲线C1:ρ=cosθ+sinθ和曲线C2:ρsin(θ﹣
 )=
)=  .
.
(1)求曲线C1和曲线C2的直角坐标方程;
(2)当θ∈(0,π)时,求曲线C1和曲线C2公共点的一个极坐标.
相关试题

