【题目】已知函数f(x)=lnx,g(x)=0.5x2﹣bx,(b为常数).
(1)函数f(x)的图象在点(1,f(1))处的切线与函数g(x)的图象相切,求实数b的值;
(2)若函数h(x)=f(x)+g(x)在定义域上不单调,求实数b的取值范围.
参考答案:
【答案】
(1)解:因为f(x)=lnx,所以 ![]() ,因此f′(1)=1,
,因此f′(1)=1,
所以函数f(x)的图象在点(1,0)处的切线方程为y=x﹣1,
由  得x2﹣2(b+1)x+2=0.
得x2﹣2(b+1)x+2=0.
由△=4(b+1)2﹣8=0,得 ![]()
(2)解:因为h(x)=f(x)+g(x)=lnx+0.5x2﹣bx(x>0),
所以 ![]() ,
,
若函数在定义域内不单调,则
可知h'(x)<0在(0,+∞)上有解,
因为x>0,设u(x)=x2﹣bx+1,因为u(0)=1>0,
则只要  解得b>2,
解得b>2,
所以b的取值范围是(2,+∞)
【解析】(1)求出f(x)的导数,可得切线的斜率和切点,可得切线的方程,联立二次函数,由判别式为0,解方程即可得到b的值;(2)求出h(x)的导数,可得h'(x)<0在(0,+∞)上有解,由二次函数的性质,可得b的不等式,即可得到b的范围.
【考点精析】利用利用导数研究函数的单调性和函数的极值与导数对题目进行判断即可得到答案,需要熟知一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方体
 的棱长为1,线段
的棱长为1,线段 上有两个动点
上有两个动点 ,且
,且 ;则下列结论错误的是( )
;则下列结论错误的是( )
A.
 B.
B.  平面
平面
C. 三棱锥
 的体积为定值 D.
的体积为定值 D.  的面积与
的面积与 的面积相等
的面积相等 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱柱
 中,
中, ,
, ,且
,且 .
.
(1)求证:
 平面
平面 ;
;(2)求证:
 平面
平面 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P-ABCD中,AB//CD,且


(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC,
 ,且四棱锥P-ABCD的体积为
,且四棱锥P-ABCD的体积为 ,求该四棱锥的侧面积.
,求该四棱锥的侧面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数
 的图象与
的图象与 轴交于点
轴交于点 ,周期是
,周期是 .
.(1)求函数解析式,并写出函数图象的对称轴方程和对称中心;
(2)已知点
 ,点
,点 是该函数图象上一点,点
是该函数图象上一点,点 是
是 的中点,当
的中点,当 ,
,  时,求
时,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 (m,n∈R)在x=1处取得极值2.
(m,n∈R)在x=1处取得极值2.
(1)求f(x)的解析式;
(2)k为何值时,方程f(x)﹣k=0只有1个根
(3)设函数g(x)=x2﹣2ax+a,若对于任意x1∈R,总存在x2∈[﹣1,0],使得g(x2)≤f(x1),求a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
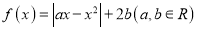 .
.(1)当
 时,解方程
时,解方程 ;
; (2)当
 时,若不等式
时,若不等式 在
在 上恒成立,求实数a的取值范围;
上恒成立,求实数a的取值范围;(3)若a为常数,且函数
 在区间
在区间 上存在零点,求实数b的取值范围.
上存在零点,求实数b的取值范围.
相关试题

