Question

【题目】驻马店市政府委托市电视台进行“创建森林城市”知识问答活动,市电视台随机对该市15～65岁的人群抽取了人,绘制出如图1所示的频率分布直方图,回答问题的统计结果如表2所示.

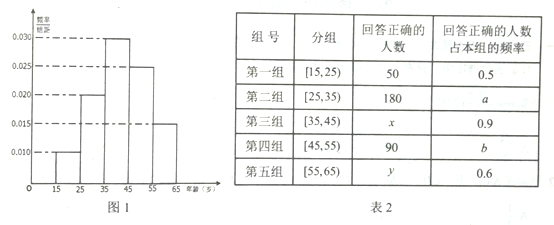
（1）分别求出的值；

（2）从第二、三、四、五组回答正确的人中用分层抽样的方法抽取7人,则从第二、三、四、五组每组回答正确的人中应各抽取多少人?

（3）在(2)的条件下,电视台决定在所抽取的7人中随机选2人颁发幸运奖,求所抽取的人中第二组至少有1人获得幸运奖的概率.

Answer 1

【答案】（1），，，；（2）2人,3人,1人,1人；（3）.

【解析】

（1）先计算出总人数为1000人，再根据公式依次计算的值.

（2）根据分层抽样规律得到从第二、三、四、五组每组回答正确的人中应分别抽取:2人,3人,1人,1人

（3）排出所有可能和满足条件的情况，得到概率.

（1）依题和图表：

由得：，

由得：，

由得：，

由得：，

由得：，

故所求，，，.

（2）由以上知:第二、三、四、五组回答正确的人数分别为:180人,270人,90人,90人

用分层抽样抽取7人,则:

从第二组回答正确的人中应该抽取: 人，

从第三组回答正确的人中应该抽取：人，

从第四组回答正确的人中应该抽取: 人，

从第五组回答正确的人中应该抽取: 人，

故从第二、三、四、五组每组回答正确的人中应分别抽取:2人,3人,1人,1人；

（3）设从第二组回答正确的人抽取的2人为: ，

从第三组回答正确的人抽取的3人为:

从第四组回答正确的人抽取的1人为:

从第五组回答正确的人抽取的1人为:

随机抽取2人,所有可能的结果有: ，，，，，，，，，，，，，，，，，，，，，共21个基本事件，其中第二组至少有1人被抽中的有：，，，，，，，，，，共这11个基本事件.

故抽取的人中第二组至少有1人获得幸运奖的概率为：.