【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以直角坐标系的原点
为参数).以直角坐标系的原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立坐标系,曲线
轴的正半轴为极轴建立坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)若过点![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,与
两点,与![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)利用平方法消去参数,即可得到![]() 的普通方程,两边同乘以
的普通方程,两边同乘以![]() 利用
利用![]() 即可得
即可得![]() 的直角坐标方程;(2)设直线
的直角坐标方程;(2)设直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),代入
为参数),代入![]() ,利用韦达定理、直线参数方程的几何意义以及三角函数的有界性可得结果.
,利用韦达定理、直线参数方程的几何意义以及三角函数的有界性可得结果.
试题解析:(1)曲线![]() 的普通方程为
的普通方程为![]() ,曲线
,曲线![]() 的直角坐标方程为
的直角坐标方程为 ![]() ;
;
(2)设直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数)
为参数)
又直线![]() 与曲线
与曲线![]() :
:![]() 存在两个交点,因此
存在两个交点,因此![]() .
.
联立直线![]() 与曲线
与曲线![]() :
:![]() 可得
可得![]() 则
则![]()
联立直线![]() 与曲线
与曲线![]() :
:![]() 可得
可得![]() ,则
,则![]()
即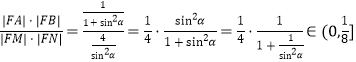
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种植园在芒果临近成熟时,随机从一些芒果树上摘下100个芒果,其质量分别在
 ,
, ,
, ,
, ,
, ,
, (单位:克)中,经统计得频率分布直方图如图所示.
(单位:克)中,经统计得频率分布直方图如图所示.
(1)现按分层抽样从质量为
 ,
, 的芒果中随机抽取
的芒果中随机抽取 个,再从这
个,再从这 个中随机抽取
个中随机抽取 个,记随机变量
个,记随机变量 表示质量在
表示质量在 内的芒果个数,求
内的芒果个数,求 的分布列及数学期望.
的分布列及数学期望.(2)以各组数据的中间数代表这组数据的平均值,将频率视为概率,某经销商来收购芒果,该种植园中还未摘下的芒果大约还有
 个,经销商提出如下两种收购方案:
个,经销商提出如下两种收购方案:A:所以芒果以
 元/千克收购;
元/千克收购;B:对质量低于
 克的芒果以
克的芒果以 元/个收购,高于或等于
元/个收购,高于或等于 克的以
克的以 元/个收购.
元/个收购.通过计算确定种植园选择哪种方案获利更多?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直四棱柱
 中,底面
中,底面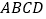 为等腰梯形,
为等腰梯形, .
.
(1)证明:
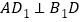 ;
;(2)设
 是线段
是线段 上的动点,是否存在这样的点
上的动点,是否存在这样的点 ,使得二面角
,使得二面角 的余弦值为
的余弦值为 ,如果存在,求出
,如果存在,求出 的长;如果不存在,请说明理由.
的长;如果不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
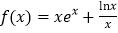 .
.(1)求证:函数
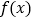 有唯一零点;
有唯一零点;(2)若对任意
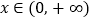 ,
,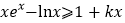 恒成立,求实数
恒成立,求实数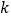 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某种植园在芒果临近成熟时,随机从一些芒果树上摘下100个芒果,其质量分别在
 ,
, ,
, ,
, ,
, ,
, (单位:克)中,经统计得频率分布直方图如图所示.
(单位:克)中,经统计得频率分布直方图如图所示.
(1) 经计算估计这组数据的中位数;
(2)现按分层抽样从质量为
 ,
, 的芒果中随机抽取
的芒果中随机抽取 个,再从这
个,再从这 个中随机抽取
个中随机抽取 个,求这
个,求这 个芒果中恰有
个芒果中恰有 个在
个在 内的概率.
内的概率.(3)某经销商来收购芒果,以各组数据的中间数代表这组数据的平均值,用样本估计总体,该种植园中还未摘下的芒果大约还有
 个,经销商提出如下两种收购方案:
个,经销商提出如下两种收购方案:A:所以芒果以
 元/千克收购;
元/千克收购;B:对质量低于
 克的芒果以
克的芒果以 元/个收购,高于或等于
元/个收购,高于或等于 克的以
克的以 元/个收购.
元/个收购.通过计算确定种植园选择哪种方案获利更多?
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
已知曲线
 的参数方程为
的参数方程为 (
( 为参数).以直角坐标系的原点
为参数).以直角坐标系的原点 为极点,
为极点, 轴的正半轴为极轴建立坐标系,曲线
轴的正半轴为极轴建立坐标系,曲线 的极坐标方程为
的极坐标方程为 .
.(1)求
 的普通方程和
的普通方程和 的直角坐标方程;
的直角坐标方程;(2)若过点
 的直线
的直线 与
与 交于
交于 ,
, 两点,与
两点,与 交于
交于 ,
, 两点,求
两点,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在四面体S﹣ABC中,SA⊥平面ABC,∠BAC=120°,SA=AC=2,AB=1,则该四面体的外接球的表面积为
A. 11π B.
 C.
C.  D.
D. 
相关试题

