【题目】某网站从春节期间参与收发网络红包的手机用户中随机抽取10000名进行调查,将受访用户按年龄分成5组:![]() 并整理得到如下频率分布直方图:
并整理得到如下频率分布直方图:
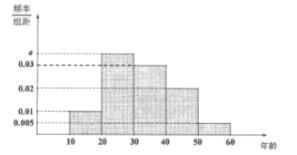
(1)求![]() 的值;
的值;
(2)从春节期间参与收发网络红包的手机用户中随机抽取一人,估计其年龄低于40岁的概率;
(3)估计春节期间参与收发网络红包的手机用户的平均年龄。
参考答案:
【答案】(1)![]() ;(2)0.75;(3)32.5
;(2)0.75;(3)32.5
【解析】分析:(1)根据频率分布直方图能求出![]() 的值.
的值.
(2)先求出样本中年龄低于40的频率,从春节期间参与收发网络红包的手机用户中随机抽取一人,由此能估计其年龄低于40岁的概率.
(3)由频率分布直方图能求出春节期间参与收发网络红包的手机用户的平均年龄估计值.
详解:
(1)根据频率分布直方图可知,![]() ,
,
解得![]() .
.
(2)根据题意,样本中年龄低于40的频率为![]() ,
,
所以从春节期间参与收发网络红包的手机用户中随机抽取一人,
估计其年龄低于40岁的概率为0.75
(3)根据题意,春季期间参与收发网络红包的手机用户的平均年龄估计为
![]() (岁)
(岁)
-
科目: 来源: 题型:
查看答案和解析>>【题目】古希腊毕达哥拉斯学派的数学家研究过各种多边形数,如三角形数1,3,6,10,…,第n个三角形数为
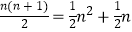 .记第n个k边形数为N(n,k)(k≥3),以下列出了部分k边形数中第n个数的表达式:
.记第n个k边形数为N(n,k)(k≥3),以下列出了部分k边形数中第n个数的表达式:
三角形数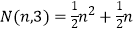 ,
,
正方形数N(n,4)=n2 ,
五边形数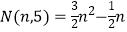 ,
,
六边形数N(n,6)=2n2﹣n,
…
可以推测N(n,k)的表达式,由此计算N(10,24)= . -
科目: 来源: 题型:
查看答案和解析>>【题目】(选修4﹣4:坐标系与参数方程)
在直角坐标系xOy中,椭圆C的参数方程为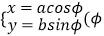 为参数,a>b>0).在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,直线l与圆O的极坐标方程分别为
为参数,a>b>0).在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,直线l与圆O的极坐标方程分别为 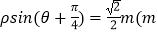 为非零常数)与ρ=b.若直线l经过椭圆C的焦点,且与圆O相切,则椭圆C的离心率为 .
为非零常数)与ρ=b.若直线l经过椭圆C的焦点,且与圆O相切,则椭圆C的离心率为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,角A,B,C对应的边分别是a,b,c,已知cos2A﹣3cos(B+C)=1.
(1)求角A的大小;
(2)若△ABC的面积S=5 ,b=5,求sinBsinC的值.
,b=5,求sinBsinC的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,抛物线
中,抛物线 的焦点为
的焦点为 ,点
,点 是抛物线
是抛物线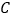 上一点,且
上一点,且 .
.(1)求
 的值;
的值;(2)若
 为抛物线
为抛物线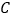 上异于
上异于 的两点,且
的两点,且 .记点
.记点 到直线
到直线 的距离分别为
的距离分别为 ,求
,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分12分)
已知函数
 ,其中
,其中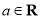 .
.(Ⅰ)当
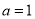 时,求曲线
时,求曲线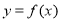 在点
在点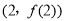 处的切线方程;
处的切线方程;(Ⅱ)当
 时,求函数
时,求函数 的单调区间与极值.
的单调区间与极值. -
科目: 来源: 题型:
查看答案和解析>>【题目】等差数列
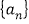 中,
中, ,
,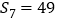 .若记
.若记 表示不超过
表示不超过 的最大整数,(如
的最大整数,(如 ).令
).令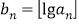 ,则数列
,则数列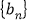 的前2000项和为__________.
的前2000项和为__________.
相关试题

