【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 的焦点为
的焦点为![]() ,点
,点![]() 是抛物线
是抛物线![]() 上一点,且
上一点,且![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() 为抛物线
为抛物线![]() 上异于
上异于![]() 的两点,且
的两点,且![]() .记点
.记点![]() 到直线
到直线![]() 的距离分别为
的距离分别为![]() ,求
,求![]() 的值.
的值.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】分析:(1)利用抛物线的定义求p的值.(2)先求出a的值,再联立直线的方程和抛物线的方程得到韦达定理,再求![]() |(y1+2) (y2+2)|的值.
|(y1+2) (y2+2)|的值.
详解:(1)因为点A(1,a) (a>0)是抛物线C上一点,且AF=2,
所以![]() +1=2,所以p=2.
+1=2,所以p=2.
(2)由(1)得抛物线方程为y2=4x.
因为点A(1,a) (a>0)是抛物线C上一点,所以a=2.
设直线AM方程为x-1=m (y-2) (m≠0),M(x1,y1),N(x2,y2).
由![]() 消去x,得y2-4m y+8m-4=0,
消去x,得y2-4m y+8m-4=0,
即(y-2)( y-4m+2)=0,所以y1=4m-2.
因为AM⊥AN,所以-![]() 代m,得y2=-
代m,得y2=-![]() -2,
-2,
所以d1d2=|(y1+2) (y2+2)|=|4m×(-![]() )|=16.
)|=16.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(选修4﹣4:坐标系与参数方程)
在直角坐标系xOy中,椭圆C的参数方程为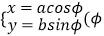 为参数,a>b>0).在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,直线l与圆O的极坐标方程分别为
为参数,a>b>0).在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,直线l与圆O的极坐标方程分别为 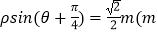 为非零常数)与ρ=b.若直线l经过椭圆C的焦点,且与圆O相切,则椭圆C的离心率为 .
为非零常数)与ρ=b.若直线l经过椭圆C的焦点,且与圆O相切,则椭圆C的离心率为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,角A,B,C对应的边分别是a,b,c,已知cos2A﹣3cos(B+C)=1.
(1)求角A的大小;
(2)若△ABC的面积S=5 ,b=5,求sinBsinC的值.
,b=5,求sinBsinC的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某网站从春节期间参与收发网络红包的手机用户中随机抽取10000名进行调查,将受访用户按年龄分成5组:
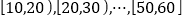 并整理得到如下频率分布直方图:
并整理得到如下频率分布直方图: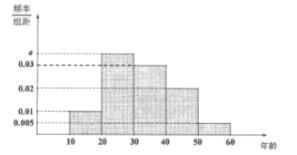
(1)求
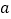 的值;
的值;(2)从春节期间参与收发网络红包的手机用户中随机抽取一人,估计其年龄低于40岁的概率;
(3)估计春节期间参与收发网络红包的手机用户的平均年龄。
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分12分)
已知函数
 ,其中
,其中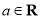 .
.(Ⅰ)当
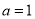 时,求曲线
时,求曲线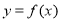 在点
在点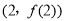 处的切线方程;
处的切线方程;(Ⅱ)当
 时,求函数
时,求函数 的单调区间与极值.
的单调区间与极值. -
科目: 来源: 题型:
查看答案和解析>>【题目】等差数列
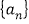 中,
中, ,
,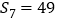 .若记
.若记 表示不超过
表示不超过 的最大整数,(如
的最大整数,(如 ).令
).令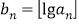 ,则数列
,则数列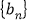 的前2000项和为__________.
的前2000项和为__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
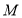 :
: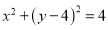 ,点
,点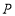 是直线
是直线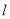 :
: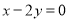 上的一动点,过点
上的一动点,过点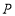 作圆M的切线
作圆M的切线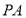 、
、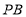 ,切点为
,切点为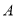 、
、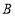 .
.(Ⅰ)当切线PA的长度为
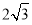 时,求点
时,求点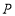 的坐标;
的坐标;(Ⅱ)若
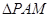 的外接圆为圆
的外接圆为圆 ,试问:当
,试问:当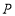 运动时,圆
运动时,圆 是否过定点?若存在,求出所有的定点的坐标;若不存在,说明理由;
是否过定点?若存在,求出所有的定点的坐标;若不存在,说明理由;(Ⅲ)求线段
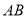 长度的最小值.
长度的最小值.
相关试题

