【题目】已知集合A={x∈R|x2-ax+b=0},B={x∈R|x2+cx+15=0},A∩B={3},A∪B={3,5}.
(1)求实数a,b,c的值;
(2)设集合P={x∈R|ax2+bx+c≤7},求集合P∩Z.
参考答案:
【答案】(1) a=6,b=9,c=-8;(2) {-2,-1,0,1}
【解析】
(1)因为A∩B={3},所以3∈B,所以32+3c+15=0即得c=-8. 因为A∩B={3},A∪B={3,5},所以A={3},所以方程x2-ax+b=0有两个相等的实数根都是3,从而求出a,b的值.(2)先求出P=![]() -
-![]() ≤x≤1},再求集合P∩Z.
≤x≤1},再求集合P∩Z.
(1)因为A∩B={3},所以3∈B,所以32+3c+15=0,c=-8,所以B={x∈R|x2-8x+15=0}={3,5}.
又因为A∩B={3},A∪B={3,5},所以A={3},所以方程x2-ax+b=0有两个相等的实数根都是3,所以a=6,b=9,所以a=6,b=9,c=-8.
(2)不等式ax2+bx+c≤7即6x2+9x-8≤7,
所以2x2+3x-5≤0,
所以-![]() ≤x≤1,
≤x≤1,
所以P=![]() -
-![]() ≤x≤1},
≤x≤1},
所以P∩Z=![]() -
-![]() ≤x≤1}∩Z={-2,-1,0,1}.
≤x≤1}∩Z={-2,-1,0,1}.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从甲、乙两品种的棉花中各抽测了25根棉花的纤维长度(单位:mm),得到如图5的茎叶图,整数位为茎,小数位为叶,如27.1mm的茎为27,叶为1.

(1)试比较甲、乙两种棉花的纤维长度的平均值的大小及方差的大小;(只需写出估计的结论,不需说明理由)
(2)将棉花按纤维长度的长短分成七个等级,分级标准如表:

试分别估计甲、乙两种棉花纤维长度等级为二级的概率;
(3)为进一步检验甲种棉花的其它质量指标,现从甲种棉花中随机抽取4根,记
 为抽取的棉花纤维长度为二级的根数,求
为抽取的棉花纤维长度为二级的根数,求 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合P={x|a+1≤x≤2a+1},Q={x|x2-3x≤10}.
(1)若a=3,求(RP)∩Q;
(2)若P∪Q=Q,求实数a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
 ,
, 是双曲线C:
是双曲线C: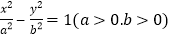 的左,右焦点,O是坐标原点
的左,右焦点,O是坐标原点 过
过 作C的一条渐近线的垂线,垂足为P,若
作C的一条渐近线的垂线,垂足为P,若 ,则C的离心率为
,则C的离心率为

A.
 B. 2 C.
B. 2 C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)若
 时,对任意的
时,对任意的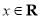 都成立,求实数
都成立,求实数 的取值范围;
的取值范围;(2)求关于
 的不等式
的不等式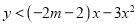 的解集.
的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】某玩具所需成本费用为P元,且P=1 000+5x+
 x2,而每套售出的价格为Q元,其中Q(x)=a+
x2,而每套售出的价格为Q元,其中Q(x)=a+ (a,b∈R),
(a,b∈R),(1)问:玩具厂生产多少套时,使得每套所需成本费用最少?
(2)若生产出的玩具能全部售出,且当产量为150套时利润最大,此时每套价格为30元,求a,b的值.(利润=销售收入-成本).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数f(x)=ax2+bx+c(a,b,c∈R)满足:对任意实数x,都有f(x)≥x,且当x∈(1,3)时,有f(x)≤
 (x+2)2成立.
(x+2)2成立.(1)证明:f(2)=2;
(2)若f(-2)=0,求f(x)的表达式;
(3)设g(x)=f(x)-
 x,x∈[0,+∞),若g(x)图象上的点都位于直线y=
x,x∈[0,+∞),若g(x)图象上的点都位于直线y= 的上方,求实数m的取值范围.
的上方,求实数m的取值范围.
相关试题

