【题目】已知F1 , F2分别是长轴长为2 ![]() 的椭圆C:
的椭圆C: ![]() +
+ ![]() =1(a>b>0)的左右焦点,A1 , A2是椭圆C的左右顶点,P为椭圆上异于A1 , A2的一个动点,O为坐标原点,点M为线段PA2的中点,且直线PA2与OM的斜率之积恒为﹣
=1(a>b>0)的左右焦点,A1 , A2是椭圆C的左右顶点,P为椭圆上异于A1 , A2的一个动点,O为坐标原点,点M为线段PA2的中点,且直线PA2与OM的斜率之积恒为﹣ ![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设过点F1且不与坐标轴垂直的直线l交椭圆于A,B两点,线段AB的垂直平分线与x轴交于点N,点N横坐标的取值范围是(﹣ ![]() ,0),求线段AB长的取值范围.
,0),求线段AB长的取值范围.
参考答案:
【答案】解:(Ⅰ)由题意可知2a=2 ![]() ,则a=
,则a= ![]() ,设P(x0 , y0),
,设P(x0 , y0),
∵直线PA与OM的斜率之积恒为﹣ ![]() ,∴
,∴ ![]() ×
× ![]() =﹣
=﹣ ![]() ,
,
∴ ![]() +
+ ![]() =1,
=1,
∴b=1,
椭圆C的方程 ![]() ;
;
(Ⅱ)设直线l:y=k(x+1),A(x1 , y1),B(x2 , y2),
联立直线与椭圆方程: 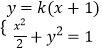 ,得:(2k2+1)x2+4k2x+2k2﹣2=0,
,得:(2k2+1)x2+4k2x+2k2﹣2=0,
则x1+x2=﹣ ![]() ,x1x2=
,x1x2= ![]() ,
,
则y1+y2=k(x1+x2+2)= ![]() ,
,
∴AB中点Q(﹣ ![]() ,
, ![]() ),
),
QN直线方程为:y﹣ ![]() =﹣
=﹣ ![]() (x+
(x+ ![]() )=﹣
)=﹣ ![]() x﹣
x﹣ ![]() ,
,
∴N(﹣ ![]() ,0),由已知得﹣
,0),由已知得﹣ ![]() <﹣
<﹣ ![]() <0,
<0,
∴0<2k2<1,
∴|AB|= ![]()
![]() =
= ![]()
![]()
= ![]()
![]() =
= ![]() (1+
(1+ ![]() ),
),
∵ ![]() <<12k2+1<1,
<<12k2+1<1,
∴|AB|∈( ![]() ,2
,2 ![]() ),
),
线段AB长的取值范围( ![]() ,2
,2 ![]() )
)
【解析】(Ⅰ)利用椭圆Q的长轴长为2 ![]() ,求出a=
,求出a= ![]() ,设P(x0 , y0),通过直线PA与OM的斜率之积恒为,﹣
,设P(x0 , y0),通过直线PA与OM的斜率之积恒为,﹣ ![]() .化简求出b,即可得到椭圆方程;(Ⅱ)将直线方程代入椭圆方程,由此利用韦达定理、中点坐标公式、直线方程、弦长公式,能求出线段AB长的取值范围.
.化简求出b,即可得到椭圆方程;(Ⅱ)将直线方程代入椭圆方程,由此利用韦达定理、中点坐标公式、直线方程、弦长公式,能求出线段AB长的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知奇函数f(x)=
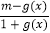 的定义域为R,其中g(x)为指数函数,且过定点(2,9).
的定义域为R,其中g(x)为指数函数,且过定点(2,9).(1)求函数f(x)的解析式;
(2)若对任意的t∈[0,5],不等式f(t2+2t+k)+f(-2t2+2t-5)>0恒成立,求实数k的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
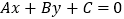 ,
,(1)系数为什么值时,方程表示通过原点的直线;
(2)系数满足什么关系时与坐标轴都相交;
(3)系数满足什么条件时只与x轴相交;
(4)系数满足什么条件时是x轴;
(5)设
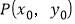 为直线
为直线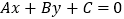 上一点,证明:这条直线的方程可以写成
上一点,证明:这条直线的方程可以写成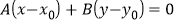
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为正方形,PA⊥底面ABCD,AD=AP,E为棱PD中点.

(1)求证:PD⊥平面ABE;
(2)若F为AB中点, ,试确定λ的值,使二面角P﹣FM﹣B的余弦值为
,试确定λ的值,使二面角P﹣FM﹣B的余弦值为  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某企业根据供销合同生产某种型号零件10万件,规定:零件长度(单位:毫米)在区间
 内,则为一等品;若长度在
内,则为一等品;若长度在 或
或 内,则为二等品;否则为不合格产品.现从生产出的零件中随机抽取100件作样本,其长度数据的频率分布直方图如图所示.
内,则为二等品;否则为不合格产品.现从生产出的零件中随机抽取100件作样本,其长度数据的频率分布直方图如图所示.(1)试估计该样本的平均数;
(2)根据合同,企业生产的每件一等品可获利10元,每件二等品可获利8元,每件不合格产品亏损6元,若用样本估计总体,试估算该企业生产这批零件所获得的利润.

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两人玩卡片游戏:他们手里都拿着分别标有数字1,2,3,4,5,6的6张卡片,各自从自己的卡片中随机抽出1张,规定两人谁抽出的卡片上的数字大,谁就获胜,数字相同则为平局.
(1)求甲获胜的概率.
(2)现已知他们都抽出了标有数字6的卡片,为了分出胜负,他们决定从手里剩下的卡片中再各自随机抽出1张,若他们这次抽出的卡片上数字之和为偶数,则甲获胜,否则乙获胜.请问:这个规则公平吗,为什么 ?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
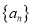 的前
的前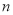 项和为
项和为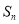 ,
,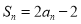 .
.(1)求数列
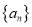 的通项公式;
的通项公式;(2)设
 ,
,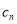 =
=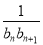 ,记数列
,记数列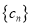 的前
的前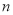 项和
项和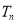 .若对
.若对 ,
, 恒成立,求实数
恒成立,求实数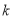 的取值范围.
的取值范围.
相关试题

